
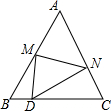
 如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{△BMD的面积}{△CDN的面积}$的值为$\frac{25}{49}$.
如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{△BMD的面积}{△CDN的面积}$的值为$\frac{25}{49}$. 分析 由BD:DC=1:3,可设BD=a,则CD=3a,根据等边三角形的性质和折叠的性质可得:BM+MD+BD=5a,DN+NC+DC=7a,再通过证明△BMD∽△CDN即可证明AM:AN的值.
解答 解:∵BD:DC=1:3,
∴设BD=a,则CD=3a,
∵△ABC是等边三角形,
∴AB=BC=AC=4a,∠ABC=∠ACB=∠BAC=60°,
由折叠的性质可知:MN是线段AD的垂直平分线,
∴AM=DM,AN=DN,
∴BM+MD+BD=5a,DN+NC+DC=7a,
∵∠MDN=∠BAC=∠ABC=60°,
∴∠NDC+∠MDB=∠BMD+∠MBD=120°,
∴∠NDC=∠BMD,
∵∠ABC=∠ACB=60°,
∴△BMD∽△CDN,
∴(BM+MD+BD):(DN+NC+CD)=AM:AN,
即AM:AN=5:7,
∴MD:ND=5:7
∴$\frac{△BMD的面积}{△CDN的面积}$=$(\frac{MD}{ND})^{2}$=($\frac{5}{7}$)=$\frac{25}{49}$,
故答案为:$\frac{25}{49}$.
点评 本题考查了等边三角形的性质、相似三角形的判定和性质以及折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,熟记这一性质是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
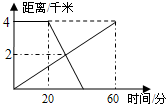 已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,下列四个说法中正确的有( )
已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,下列四个说法中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
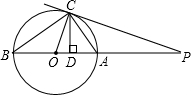 如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.
如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
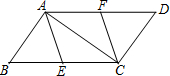 如图,已知点E,F分别是?ABCD的边BC、AD上的中点,且∠BAC=90°,
如图,已知点E,F分别是?ABCD的边BC、AD上的中点,且∠BAC=90°,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
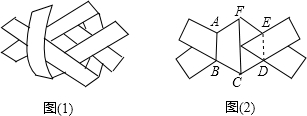 用两条宽均为2cm的纸条(假设纸条的长度足够长),折叠穿插,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正六边形ABCDEF,则折出的正六边形的边长为$\frac{4\sqrt{3}}{3}$cm.
用两条宽均为2cm的纸条(假设纸条的长度足够长),折叠穿插,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正六边形ABCDEF,则折出的正六边形的边长为$\frac{4\sqrt{3}}{3}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com