【题目】解下列方程
(1)2x2-4x-10=0 (用配方法)
(2)2x2+3x=4(公式法)
(3)(x-2)2=2(x-2)
(4)
【答案】(1)
，
；(2)
，
；(3)x1=2，x2=4；(4)
，
.
【解析】
（1）用配方法求解即可；
（2）用公式法求解即可；
（3）移项后用因式分解法求解即可；
（4）用公式法求解即可.
(1) ∵2x2-4x-10=0 ，
∴2x2-4x=10 ，
∴x2-2x=5 ，
∴x2-2x+1=5+1 ，
∴(x-1)2=6，
∴x-1=
，
∴，；
(2) ∵2x2+3x=4，
∴2x2+3x-4=0，
∵a=2,b=3,c=-4,
∴=9+32=41,
∴
,
∴，；
(3) ∵(x-2)2=2(x-2)，
∴(x-2)2-2(x-2)=0，
∴(x-2) (x-2-2)=0,
∴x-2=0或x-4=0，
∴x1=2，x2=4；
(4)
，
∵a=
,b=3,c=-2,
∴=9+16=25，
∴x=
,
∴，.
备战中考寒假系列答案科目：初中数学 来源： 题型：
【题目】若一个三位数百位上数字是
，十位上数字是
．个位上数字是
,则这个三位数可记作
(1)若一个两位数
．满足关系式
．
①试求出
的数量关系:
②请直接写出满足关系式的所有两位数．
(2)将一个三位数
,其中
．现将三位数中间数字
去掉，成为一个两位数
且满足
．请直接写出所有符合条件的三位数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+c的图象经过点A（﹣4，3），B（﹣2，6），点A关于抛物线对称轴的对称点为点C，点P是抛物线对称轴右侧图象上的一点，点G（0，﹣1）．
（1）求出点C坐标及抛物线的解析式；
（2）若以A，C，P，G为顶点的四边形面积等于30时，求点P的坐标；
（3）若Q为线段AC上一动点，过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M，将△QGM沿QG翻折得到△QGN，当点N在坐标轴上时，求Q点的坐标．
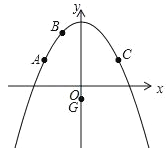
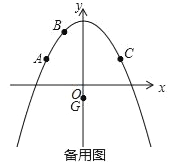
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的口袋中装有4个红球，3个白球，2个黄球，每个球除颜色外都相同．
（1）请判断下列事件是不确定事件、不可能事件还是必然事件，填写在横线上．
①从口袋中任意摸出1个球是白球；
②从口袋中任意摸出4个球全是白球；
③从口袋中任意摸出1个球是红球或黄球；
④从口袋中任意摸出8个球，红、白、黄三种颜色的球都有；
（2）请求出（1）中不确定事件的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l1：y=2x+1与直线l2：y=mx+4相交于点P（1，b）
(1)求b，m的值
(2)垂直于x轴的直线x=a与直线l1，l2分别相交于C，D，若线段CD长为2，求a的值
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A7B7A8的边长为（ ）
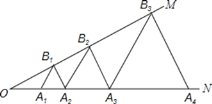
A. 64B. 32C. 16D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设直线y＝kx+6和直线y＝（k+1）x+6（k是正整数）及x轴围成的三角形面积为Sk（k＝1，2，3，…，8），则S1+S2+S3+…+S8的值是（ ）
A. 
B. 
C. 16D. 14
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数 yax 2(a0) 的图象与反比例函数 y
(k0) 的图象交于 A、B两点，且与x轴、y轴分别交于点C、D．已知 tan∠AOC=
，AO=
．
（1）求这个一次函数和反比例函数的解析式；
（2） 若点 F 是点D 关于 x 轴的对称点，求△ABF 的面积．
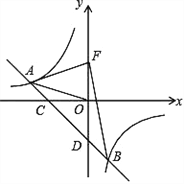
查看答案和解析>>
科目：初中数学 来源： 题型：
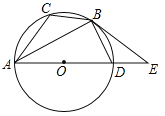
【题目】如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD=BC，延长AD到E，BE是⊙O的切线，B是切点．
（1）求证：∠EBD=∠CAB；
（2）若BC=
，AC=5，求sin∠CBA．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com