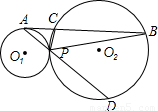
分析:(1)相切两圆常作的辅助线是:两圆的公切线,因此过点P作两圆的内公切线EP交AB于点F,然后证得△CDP∽△ADC,可证DC
2=DP•DA;
(2)求AB的长时,由(1)知△CDP∽△ADC,可得
=.还可得出DP=2PA,DC=BD.再根据切割线定理得:AP•AD=AB•AC,由此可求出AB的长.
解答: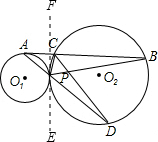
(1)证明:过点P作两圆的内公切线EP交AB于点F,
∵FE、CA都与圆O
1相切,
∴FP=FA,
∴∠FAP=∠FPA;
∵∠FPA=∠EPD=∠DCP,
∴∠FAP=∠DCP;
∵∠PDC=∠CDA,
∴△CDP∽△ADC;
∴
=;
∴DC
2=DP•DA.
(2)解:连接O
1O
2,则点P在O
1O
2上,连接O
1A、O
2D,
∵O
1A=O
1P,
∴∠O
1AP=∠O
1PA;
又∵O
2P=O
2D,
∴∠O
2DP=∠O
2PD,
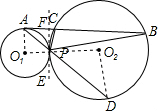
∴∠O
1AP=∠O
2DP;
∴O
1A∥O
2D,
∴
==
;
∴DP=2PA,
∵DP=12
∴PA=6,
由(1)中△CDP∽△ADC,得∠DCB=∠APC,
=;
∵∠APC=∠DBC,
∴∠DCB=∠DBC;
∴DC=BD=4
;
∵DP=12,AP=4,
∴AD=AP+DP=16;
∴
=,
∴AC=48
.
由AP•AD=AB•AC,得4×12=48
AB,
∴AB=
.
点评:此题综合性强,将圆的有关知识与三角形相似结合考查,有一定难度;命题立意:此题主要考查相切两圆的位置关系及切线长定理,三角形相似的判定等知识.

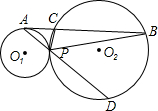 线AP交圆O2于点D,连接DC、PC.
线AP交圆O2于点D,连接DC、PC. (1)证明:过点P作两圆的内公切线EP交AB于点F,
(1)证明:过点P作两圆的内公切线EP交AB于点F,


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案 ,PD=12,求AB的长.
,PD=12,求AB的长.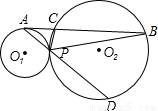
 ,PD=12,求AB的长.
,PD=12,求AB的长.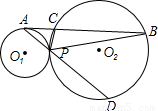
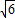 ,PD=12,求AB的长.
,PD=12,求AB的长.
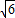 ,PD=12,求AB的长.
,PD=12,求AB的长.