
分析 ①利用不等式的基本性质,先将不等式去分母,再去括号,移项、合并同类项,最后系数化为1即可.
②先求出两个不等式的解集,再求其公共解,然后写出非负整数解.
③首先分别解出两个不等式,再根据:大大取大,小小取小,大小小大取中,大大小小取不着,确定出两个不等式的公共解集即可.
解答 解:①去分母,得-3(x-3)≥-2(x-1)+6x,
去括号,得-3x+9≥-2x+2+6x,
移项、合并同类项,得-7x≥-7,
系数化为1,得x≤1.
在数轴上表示此不等式的解集如下:
②$\left\{\begin{array}{l}{\frac{2}{3}x+5>1-x①}\\{x-1<\frac{3}{4}x-\frac{1}{8}②}\end{array}\right.$,
解不等式①得,x>-$\frac{12}{5}$,
解不等式②得,x<$\frac{7}{2}$,
所以不等式组的解集是-$\frac{12}{5}$≤x<$\frac{7}{2}$,
所以不等式组的非负整数解是0,1,2,3.
③∵6≤$\frac{3x-14}{2}-\frac{9x+2}{7}<8$,
∴$\left\{\begin{array}{l}{6≤\frac{3x-14}{2}-\frac{9x+2}{7}①}\\{\frac{3x-14}{2}-\frac{9x+2}{7}<8②}\end{array}\right.$,
由不等式①得:x≥62,
由不等式②得:x<$\frac{214}{3}$,
所以不等组的解集为:62≤x<$\frac{214}{3}$.
点评 本题主要考查了一元一次不等式(组)解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
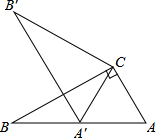 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为60°.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
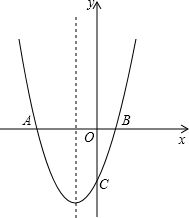 如图,抛物线y=(x+1)2+k与x轴交于A,B两点,与y轴交于点C(0,-3),抛物线的对称轴上存在一点P,使得PB+PC的值最小,求此时点P的坐标.
如图,抛物线y=(x+1)2+k与x轴交于A,B两点,与y轴交于点C(0,-3),抛物线的对称轴上存在一点P,使得PB+PC的值最小,求此时点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )| A. | 当x=2时,y=5 | B. | 矩形MNPQ的面积是20 | ||
| C. | 当x=6时,y=10 | D. | 当y=$\frac{15}{2}$时,x=10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com