
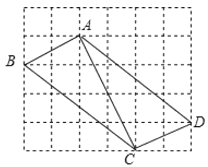
【题目】如图,在边长为1的小正方形组成的网格中,![]() 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:

(1)画线段![]() ,且使
,且使![]() ,连接
,连接![]() ;
;
(2)线段![]() 的长为________,
的长为________,![]() 的长为________,
的长为________,![]() 的长为________;
的长为________;
(3)![]() 是________三角形,四边形
是________三角形,四边形![]() 的面积是________;
的面积是________;
(4)若点![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() ,则
,则![]() 的度数为________.
的度数为________.
【答案】(1)见解析;(2)![]() ,
,![]() ,5;(3)直角,10;(4)
,5;(3)直角,10;(4)![]()
【解析】
(1)根据题意,画出AD∥BC且使AD=BC,连接CD;
(2)在网格中利用直角三角形,先求AC ![]() 的值,再求出AC的长,CD的长,AD的长;
的值,再求出AC的长,CD的长,AD的长;
(3)利用勾股定理的逆定理判断直角三角形,再求出四边形ABCD的面积;
(4)把问题转化到Rt△ACB中,利用直角三角形斜边上的中线可知BE=AE=EC,根据等腰三角形性质即可解题.
(1)如图所示:AD、CD为所求作
(2)根据勾股定理得:![]()
故答案为:![]() ;
;![]() ;5
;5
(3)∵![]() ,
,![]()
∴![]()
∴![]() 是直角三角形,∠ACD=90°
是直角三角形,∠ACD=90°
∴四边形![]() 的面积是:
的面积是:![]()
故答案为:直角;10
(4)∵![]() ,
,![]()
∴四边形ABCD是平行四边形
∴AB//CD
∴∠BAC=∠ACD=90°
在Rt△ACD中,![]() 为
为![]() 的中点
的中点
∴AE=BE=CE, ∠ABC+∠ACB=90°
∴∠ACB=∠EAC=27°
∴∠ABC =63°
故答案为:![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)![]() 为何值时,方程有一根为零?
为何值时,方程有一根为零?
(2)![]() 为何值时,方程的两个根互为相反数?
为何值时,方程的两个根互为相反数?
(3)是否存在![]() ,使方程的两个根互为倒数?若存在,请求出
,使方程的两个根互为倒数?若存在,请求出![]() 的值;不存在,请说明理由.
的值;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图①,当点D在边BC上时,且n等于30°,则∠BAD= ,∠CDE= ;
(2)如图②,当点D运动到点B左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由;
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请在图③中画出图形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数y=![]() (k>1)和y=
(k>1)和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B,BE⊥x轴于点E,当点P在y=
的图象于点B,BE⊥x轴于点E,当点P在y=![]() 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com