
【题目】如图,己知直线![]() 过
过![]() 与
与![]() 交于
交于![]() 点、
点、![]() 点,与
点,与![]() 交于
交于![]() 点,直线
点,直线![]() 与
与![]() 轴交于
轴交于![]() 点,且
点,且![]() ,则
,则![]() ________.
________.

【答案】10
【解析】
过点A作AE⊥x轴于E,过点B作BG⊥x轴于G,先利用待定系数法求得函数![]() 的解析式,再根据
的解析式,再根据![]() ,求得BG=2,从而求得B点坐标,然后用待定系数法求得一次函数的解析式,再求得C点坐标,根据对称点的性质求得E点坐标,最后求得k的值即可.
,求得BG=2,从而求得B点坐标,然后用待定系数法求得一次函数的解析式,再求得C点坐标,根据对称点的性质求得E点坐标,最后求得k的值即可.
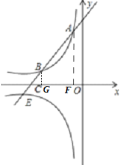 过点A作AE⊥x轴于E,过点B作BG⊥x轴于G,易得△BCG∽△ACO,
过点A作AE⊥x轴于E,过点B作BG⊥x轴于G,易得△BCG∽△ACO,
将A坐标代入反比例函数![]() ,得m=﹣6,
,得m=﹣6,
即反比例函数的解析式为![]() ,
,
∵A(﹣1,6),
∴AF=6,OF=1,
∵![]() ,
,
∴![]() ,
,
∴BG=![]() AF=2,
AF=2,
把y=2代入![]() ,
,
解得:x=﹣3,即B(﹣3,2),
将A,B坐标代入直线![]() 中得,
中得,
![]() ,
,
解得:a=2,b=8,
∴直线AB的解析式为y=2x+8,
令y=0,得到x=﹣4,即C(﹣4,0),
∵BE=2BC,
∴C为BE中点,
∴E(﹣5,﹣2),
将E坐标代入![]() ,得:k=10.
,得:k=10.
故答案为:10.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A1 、A2 、A3是抛物线y=x2上三点, A1B1 、A2B2 、A3B3 分别是垂直于x轴,垂足为B1 、B2 、B3 ,直线A2B2交线段A1A3于点C,若A1 、A2 、A3 三点的横坐标依次为1、2、3,则线段CA2的长为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图,点
如图,点![]() 是直线
是直线![]() 上方抛物线上的一动点,当
上方抛物线上的一动点,当![]() 面积最大时,请求出点
面积最大时,请求出点![]() 的坐标和
的坐标和![]() 面积的最大值?
面积的最大值?
![]() 在
在![]() 的结论下,过点
的结论下,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 是抛物线对称轴上的动点,在抛物线上是否存在点
是抛物线对称轴上的动点,在抛物线上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?如果存在,请直接写出点
为顶点的四边形是平行四边形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°.
(1)观察猜想如图1,点E在BC上,线段AE与BD的数量关系,位置关系.
(2)探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;
(3)拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在直线上时,请直接写出AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月23日,安徽省省政府新闻办召开新闻发布会,通报了2017年全省经济运行情况。据省统计局新闻发言人赵金宝介绍,去年我省GDP突破19000亿元,连续第十年保持两位数增长,增速明显高于全国,位居中部第一。初步核算,全年全省生产总值19033.3亿元,按可比价格计算,比2015年增加3303.3亿元,连续10年保持两位数增长,增幅居全国第11、中部第1位。求自2015年起的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法: ①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ①②③④ D. ①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com