
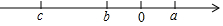 已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.分析 (1)因为a和b异号,且绝对值相等,所以a与b是互为相反数,则和a+b=0,商$\frac{a}{b}$=-1;
(2)根据数轴上a、b、c的大小关系:c<b<0<a,则:|a-c|=a-c,|c-b|=b-c,|b-a|=a-b.
解答 解:(1)∵从数轴可知:c<b<0<a,且|a|=|b|,
∴a+b=0,$\frac{a}{b}$=-1,
(2)|a-c|+|c-b|+|b-a|,
=a-c+b-c+a-b,
=2a-2c.
点评 本题考查了整式的加减,同时还考查了绝对值和数轴的定义,要明确数轴上的点右边的总比左边的大,原点右边的数为正数,原点左边的数为负数;对于绝对值要知道:正数的绝对值等于它本身,负数的绝对值等于它相反数,并能正确根据整式的加减法则进行化简.


科目:初中数学 来源: 题型:解答题
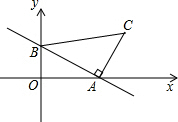 如图,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°
如图,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-4\frac{2}{3}>-4.7$ | B. | $-\frac{12}{23}<-\frac{6}{11}$ | C. | -0.2<-0.22 | D. | $-0.01<-\frac{1}{100}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.2cm 0.3m 0.4cm 0.2cm | B. | 1cm 2cm 3cm 4cm | ||
| C. | 4cm 6cm 8cm 3cm | D. | $\sqrt{2}$cm $\sqrt{6}$cm $\sqrt{8}$cm $\sqrt{7}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AC=8,AB=10,∠BAC=60°,⊙O与AB,AC都相切,与AB的切点为E.
如图,在△ABC中,AC=8,AB=10,∠BAC=60°,⊙O与AB,AC都相切,与AB的切点为E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com