
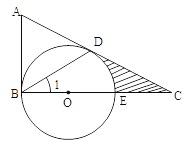
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
【答案】(1)证明见解析;(2)2![]() -
-![]() .
.
【解析】试题分析:(1)由OD=OB得∠1=∠ODB,则根据三角形外角性质得∠DOC=∠1+∠ODB=2∠1,而∠A=2∠1,所以∠DOC=∠A,由于∠A+∠C=90°,所以∠DOC+∠C=90°,则可根据切线的判定定理得到AC是⊙O的切线;
(2)解:由∠A=60°得到∠C=30°,∠DOC=60°,根据含30度的直角三角形三边的关系得CD=![]() OD=2
OD=2![]() ,然后利用阴影部分的面积=S△COD-S扇形DOE和扇形的面积公式求解.
,然后利用阴影部分的面积=S△COD-S扇形DOE和扇形的面积公式求解.
试题解析:(1)连接OD,
∵OD=OB,
∴∠1=∠ODB,
∴∠DOC=∠1+∠ODB=2∠1,
而∠A=2∠1,
∴∠DOC=∠A,
∵∠A+∠C=90°,
∴∠DOC+∠C=90°,
∴OD⊥DC,
∴AC是⊙O的切线;
(2)∵∠A=60°,
∴∠C=30°,∠DOC=60°,
在Rt△DOC中,OD=2,
∴CD=![]() OD=2
OD=2![]() ,
,
∴阴影部分的面积=S△COD-S扇形DOE
=![]() ×2×2
×2×2![]() -
-![]()
=2![]() -
-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH. 
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两厂在公路的同侧,现欲在公路边建一货场C.
(1)若要使货场到两厂的距离相等,请在图1中作出此时货场的位置.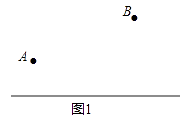
(2)若要求所修公路(即A、B两厂到货场的距离之和)最短,请在图2中作出货场的位置.(用尺规作图,保留作图痕迹,不必写作法)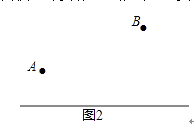
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题. 大家知道 ![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 ![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 ![]() ﹣1来表示
﹣1来表示 ![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为 ![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:已知10+ ![]() =x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
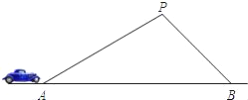
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/时=
≈1.73,60千米/时=![]() 米/秒)
米/秒)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,不正确的是( )
A.对角线相等的矩形是正方形B.对角线垂直平分的四边形是菱形
C.矩形的对角线平分且相等D.顺次连结菱形各边中点所得的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表:
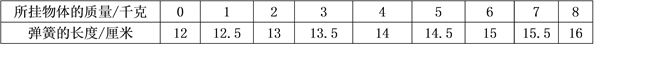
(1)上表中,自变量是 ,因变量是 ;
(2)弹簧不挂物体的长度是 ;
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是 ,写出y与x的关系式 ;
(4)如果弹簧最大挂质量为25千克,你能计算出当挂重为14千克时,弹簧的长度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com