
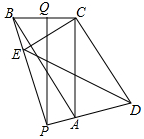
 如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求:
如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求:分析 (1)设∠BCE=∠ACD=α,可得∠CBE=∠CEB=∠CAD=∠CDA=90°-$\frac{1}{2}$α,根据四边形内角和可得∠BPA=90°;
(2)取AB的中点K,连接PK、QK,则KQ=$\frac{1}{2}$AC=4,PK=AB=5,继而可得PQ≤KP+KQ=9.
解答 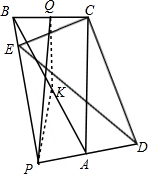 解:(1)∵△DEC是由△ABC绕C点旋转得到,
解:(1)∵△DEC是由△ABC绕C点旋转得到,
∴CE=CB,CD=CA,∠BCE=∠ACD,
设∠BCE=∠ACD=α∴∠CBE=∠CEB=∠CAD=∠CDA=90°-$\frac{1}{2}$α,
∴在四边形BCDP中,∠BPA=360°-90°-α-2(90°-$\frac{1}{2}$α)=90°;
(2)∵在RT△ABC中,∠ACB=90°,BC=6,AC=8,
∴AB=10,
如图,取AB的中点K,连接PK、QK,
则KQ=$\frac{1}{2}$AC=4,PK=AB=5,
∴PQ≤KP+KQ=9,
∴PQ的最大值是9.
点评 本题主要考查旋转的性质、直角三角形的性质及勾股定理、中位线定理,构建以PQ为边的三角形,根据三角形三边关系得出PQ的长度范围是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按要求作图,不必写作图过程,但必须保留作图痕迹.
按要求作图,不必写作图过程,但必须保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
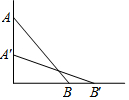 如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.
如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -|-2|=2 | B. | (6.4×106)÷(8×103)=800 | ||
| C. | (-1)2015-12016=-2 | D. | $-6÷({\frac{1}{3}-\frac{1}{2}})=36$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
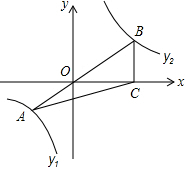 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com