
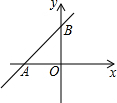 如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点.
如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点.分析 (1)令x=0得y=3,令y=0得x=-4,由此即可解决问题.
(2)画出图形,求出点B′坐标,利用待定系数法即可求出直线AB′的解析式.
(3)旋转过程中点B所经过的路径是以点A为圆心,AB为半径的弧,利用弧长公式计算即可.
解答 解:(1)令x=0得y=3,令y=0得x=-4,
∴点A(-4,0),点B(0,3).
故答案为A(-4,0),B(0,3).
(2)△AOB绕点A顺时针旋转90°后得到△AO′B′,图象如图所示,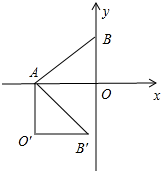
∵A(-4,0),B′(-1,-4)设直线AB′的解析式为y=kx+b,则有$\left\{\begin{array}{l}{-4k+b=0}\\{-k+b=-4}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-\frac{16}{3}}\end{array}\right.$,
∴直线AB′解析式为y=-$\frac{4}{3}$x-$\frac{16}{3}$.
(3)∵OA=4,OB=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴旋转过程中点B所经过的路径长是$\frac{1}{4}$π•52=$\frac{25}{4}$π.
点评 本题考查轨迹、旋转变换、一次函数等知识,解题的关键是灵活应用待定系数法确定函数解析式,需要记住弧长公式,属于中考常考题型.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我校在12月刚刚举办了初一初二年级的青春艺术节,高质量的表演引起了极大的反响,重庆演艺集团决定后期在八中开展“高雅艺术进学校”的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在某年级学生中进行随机抽样调查(四个选项中必须且只选一项),根据调查统计结果,绘制了两种不完整的统计图表:
我校在12月刚刚举办了初一初二年级的青春艺术节,高质量的表演引起了极大的反响,重庆演艺集团决定后期在八中开展“高雅艺术进学校”的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在某年级学生中进行随机抽样调查(四个选项中必须且只选一项),根据调查统计结果,绘制了两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 唱歌 | 35% |
| B | 舞蹈 | a |
| C | 绘画 | 25% |
| D | 演讲 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连结EF、BF,EF与对角线AC交于点O,且BE=BF,∠DFE=2∠ACF.
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连结EF、BF,EF与对角线AC交于点O,且BE=BF,∠DFE=2∠ACF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们把依次连结任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,依次连结各边中点得到的中点四边形EFGH.
我们把依次连结任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,依次连结各边中点得到的中点四边形EFGH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com