
分析 分二次项系数为0或非0两种情况考虑,当a-2=0时,解一元一次方程求出x的值,可得a=2符合题意;当a-2≠0时,根据方程有实数根结合根的判别式即可得出关于a的一元一次不等式,解不等式可得出a的取值范围.综上即可得出结论.
解答 解:当a-2=0,即a=2时,原方程为:-4x-1=0,
解得:x=-$\frac{1}{4}$,
∴a=2符合题意;
当a-2≠0,即a≠2时,
∵方程(a-2)x2-4x-1=0有实数根,
∴△=(-4)2-4×(a-2)×(-1)=4a+8≥0,
解得:a≥-2且a≠2.
综上可知:a的取值范围为a≥-2.
故答案为:a≥-2.
点评 本题考查了根的判别式,分二次项系数为0或非0两种情况考虑是解题的关键.


科目:初中数学 来源: 题型:解答题
 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
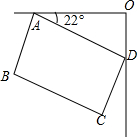 家用电冰箱在使用过程中能有效地散热是节电的有效途径之一.将一台家用电冰箱置于厨房的墙角,如图是它的俯视图,∠DAO=22°,冰箱的后背AD=110cm,AD平行于前沿BC,且与BC的距离为60cm,则从墙角O到前沿BC的距离约为(精确到1cm)( )
家用电冰箱在使用过程中能有效地散热是节电的有效途径之一.将一台家用电冰箱置于厨房的墙角,如图是它的俯视图,∠DAO=22°,冰箱的后背AD=110cm,AD平行于前沿BC,且与BC的距离为60cm,则从墙角O到前沿BC的距离约为(精确到1cm)( )| A. | 97cm | B. | 98cm | C. | 99cm | D. | 100cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com