
����Ŀ���߳�Ϊ2��������OABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����D�DZ�OA���е㣬����CD���� E�ڵ�һ���ޣ���DE��DC��DE=DC����ֱ��ABΪ�Գ���������߹�C��E���㣮
��1����E�����ꣻ
��2���������ߵĽ���ʽΪy=a��x��h��2+k����a��h��k��
��3����MΪֱ��AB��һ���㣬��NΪ��������һ���㣬�Ƿ���ڵ�M��N��ʹ���Ե�M��N��D��EΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�����������ĵ�M��N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����E��EF��x���ڵ�F����ͼ1��
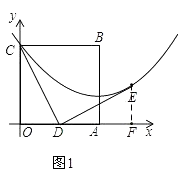
��DE��DC��
���CDO+��EDF=90�㣬
�ߡ�CDO+��OCD=90�㣬
���OCD=��EDF��
�ڡ�COD�͡�DFE��

���COD�ա�DFE��AAS����
��OD=EF��DF=CO��
��CO=OA=2��DΪOA�е㣬
��EF=OD=DA=1��DF=OC=2��
��E��3��1��
��2��
�⣺��������y=a��x��h��2+k��ABΪ�Գ��ᣬ
��h=2��
��y=a��x��h��2+k����C��0��2����E��3��1�����㣬
�� ![]() ��
��
��ã� ![]()
��3��
�⣺������DEΪƽ���ı��εĶԽ��ߣ���ͼ2��

��ʱ��N����������ߵĶ��㣨2�� ![]() ����
����
��N��E������������ֱ��NE�Ľ���ʽΪ��y= ![]() x��
x��
��DM��EN��
����DM�Ľ���ʽΪ��y= ![]() ��
��
��D��1��0����������b=�� ![]() ��
��
��DM�Ľ���ʽΪ��y= ![]() ��
��
��x=2����y= ![]() ��
��
��M��2�� ![]() ����
����
�ڹ���C��CM��DE�������߶Գ����ڵ�M������ME����ͼ3��

��CM��DE��DE��CD��
��CM��CD��
��OC��CB��
���OCD=��BCM��
�ڡ�OCD�͡�BCM��
 ��
��
���OCD�ա�BCM��ASA����
��CM=CD=DE��BM=OD=1��
��CDEM��ƽ���ı��Σ�
��N����Cռ�غϣ�
��N��0��2����M��2��3����
��N���������߶Գ����Ҳ࣬MN��DE����ͼ4��

��NG��BA�ڵ�G���ӳ�DM��BN�ڵ�H��
��MNED��ƽ���ı��Σ�
���MDE=MNE����ENH=��DHB��
��BN��DF��
���ADH=��DHB=��ENH��
���MNB=��EDF��
�ڡ�BMN�͡�FED��

���BMN�ա�FED��AAS����
��BM=EF=1��
BN=DF=2��
��M��2��1����N��4��2����
����������N��M�ֱ��������ʱ���Ե�M��N��D��EΪ������ı�����ƽ���ı���
N��2�� ![]() ����M��2��
����M��2�� ![]() ����
����
N��0��2����M��2��3����
M��2��1����N��4��2��
����������1������E��EF��x���ڵ�F��֤��COD�ա�DFE���ɣ���2��ֱ��AB���ǶԳ��ᣬȷ����h�����C��E�������꣬���������߽���ʽ��ȷ��a��k����3��������������ۣ�N�������߶��㴦��N�������߶Գ�����ࣻN�������߶Գ����Ҳ࣮


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ٰ��˶��ᣬ��1500����Ŀ�У�����ѡ����200�Ļ����ܵ��Ͻ��У���ͼ��¼���ܵ�����һλѡ����������һλѡ�ֵ��ܲ�ȫ���̣����˶�������ȫ�̣�������x������������ѡ��ȫ�̵��ܲ�ʱ�䣬y������������λѡ��֮��ľ��룬����˵���������ǣ�������
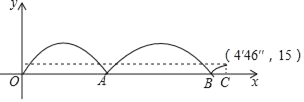
A. ����������ѡ����������ѡ������������
B. ����������ѡ����������ѡ�ֵ�һ�������ȵڶ�����������ʱ��
C. ����ѡ�ֵ����յ�ʱ��������ѡ�ֻ���415��δ��
D. �ܵ�������ѡ����ʱ4��46��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������Rt��ABC�У���ABC=90�㣬AB=BC��DΪб��AC�ӳ�����һ�㣬��D����BC�Ĵ��߽����ӳ����ڵ�E����AB���ӳ�����ȡһ��F��ʹ��BF=CE������EF��
��1����AB=2��BF=3����AD�ij��ȣ�
��2��GΪAC�е㣬����GF����֤����AFG+��BEF=��GFE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������L��y=ax2+bx+c��x�ύ��A��B��3��0�����㣨A��B����ࣩ����y�ύ�ڵ�C��0��3������֪�Գ���x=1��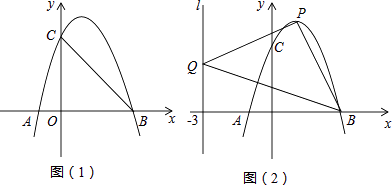
��1����������L�Ľ���ʽ��
��2����������L����ƽ��h����λ���ȣ�ʹƽ�ƺ����������ߵĶ������ڡ�OBC�ڣ�������OBC�ı߽磩����h��ȡֵ��Χ��
��3�����P��������L����һ�㣬��Q��ֱ��l��x=��3�ϣ���PBQ�ܷ��Ϊ�Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ����ܣ�������������ĵ�P�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=10��OC=8����OC����ȡһ��D����ֽƬ��AD���ۣ�ʹ��O����BC���ϵĵ�E������D��E��������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ��,![]() ����
����![]() .
.
(1)��![]() ��ֵ;
��ֵ;
(2)����![]() ����������ϴ���һ��
����������ϴ���һ��![]() ��ʹ
��ʹ![]() �����
�����![]() ������;
������;
������������һ�����ڶ��ٸ���![]() ��ʹ
��ʹ![]() ����?��ֱ��д�����������ĵ�
����?��ֱ��д�����������ĵ�![]() ������.
������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У�DC=6cm����DC�ϴ���һ��E����ֱ��AE��������AE�۵���ʹ��Dǡ������BC���ϣ���˵�ΪF����������ABF�����Ϊ24����ôCE����Ϊ__________cm2.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ABC����ĺᡢ�����궼��������������ABC��ij��Ϊ��ת���ģ�˳ʱ����ת90��õ���DEF������ת���ĵ������ǣ� ��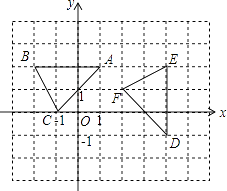
A.��0��0��
B.��1��0��
C.��1����1��
D.��2.5��0.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC����������ֱ���A����3��2����B��0��4����C��0��2����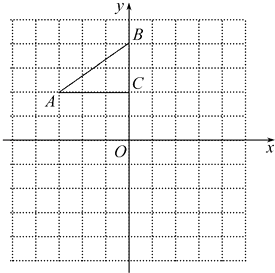
��1������ABC�Ե�OΪ��ת������ת90�㣬�뻭����ת��ġ�A��B��C�䣻
��2����x������һ��P��ʹ��PA+PB��ֵ��С����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com