练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
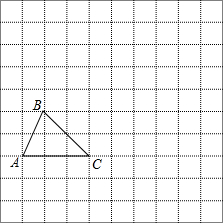
    6．如图，在边长为1的小正方形组成的网络中，△ABC的顶点均在格点上，请按要求完成下列各题：
    （1）以直线AC为对称轴作△ABC的轴对称图形，得到△AB1C，再将△ABC绕着点C顺时针旋转90°，得到△A2B2C，请依次画出△AB1C、△A2B2C；
    （2）请画出一个格点△A3B3C3，使△A3B3C3∽△ABC，且相似比不为1．

    分析 （1）根据轴对称的性质画出△AB1C，再由图形旋转的性质得到△A2B2C即可；
    （2根据三角形相似的性质画出格点△A3B3C3即可．

    解答 解：（1）如图所示，△AB1C，△A2B2C即为所求；

    （2）如图所示，△A3B3C3即为所求．

    点评 本题考查的是作图-旋转变换，熟知图形旋转不变性的性质是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如图，△ABC中，∠1=∠A，∠2=∠C，∠ABC=∠C，求∠ADB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．点P位于x轴上方，y轴左侧，距离x轴4个单位长度，距离y轴2个单位长度，那么点P的坐标是（　　）
    A．（4，2）B．（-2，4）C．（-4，2）D．（2，4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

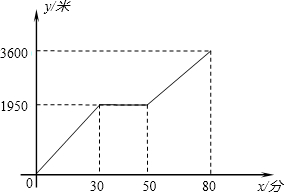    14．小华和小晶上山游玩，小华步行，小晶乘坐缆车，相约在山顶缆车的终点会合．已知小华步行的路程是缆车所经线路长的2倍，小晶在小华出发后50分钟才坐上缆车，缆车的平均速度为每分钟180米．图中的折线反映了小华行走的路程y（米）与时间x（分钟）之间的函数关系．
    （1）小华行走的总路程是3600米，他途中休息了20分钟；
    （2）当0≤x≤30时，y与x的函数关系式是y=65x；
    （3）小华休息之后行走的速度是每分钟55米；
    （4）当小晶到达缆车终点时，小华离缆车终点的路程是1100米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．某公用电话亭打电话时，需付电话费y（元）与通话时间x（分钟）之间的函数图象如图所示，则小明打了8分钟电话需付话费2.6元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

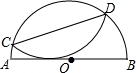    11．半圆⊙O中，AB为直径，C、D为半圆上任意两点，将$\widehat{CD}$沿直线CD翻折使AB与$\widehat{CD}$相切，已知AB=8，求CD的最大值4$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

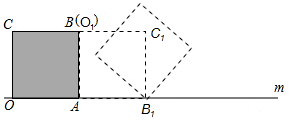
    18．小慧把边长为1的正方形纸片0ABC放在直线l2上，0A边与直线l2重合，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时点O运动到了点O1处（即点B处），点C运动到了点C1处，点B运动到了点B2处，小慧又将正方形纸片 AO1C1B1绕顶点B1按顺时针方向旋转90°，…．正方形纸片OABC按上述方法经过81次旋转，顶点0经过的路程是$\frac{{41+20\sqrt{2}}}{2}π$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．x与6的和一半是非负数，用不等式表示为（　　）
    A．$\frac{1}{2}$（x+6）≥0B．$\frac{1}{2}$x+6≤0C．$\frac{1}{2}$x+6≥0D．$\frac{1}{2}$（x+6）≤0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．$\frac{1}{4}$的算术平方根是（　　）
    A．$\frac{1}{2}$B．-$\frac{1}{2}$C．${\;}_{-}^{+}$$\frac{1}{2}$D．$\frac{1}{16}$

    查看答案和解析>>

    同步练习册答案