Question

18．枣庄市举行“小哥白尼杯”中学生创新实践大赛，所有参赛学生分别设有一、二、三等奖和纪念奖，获奖情况已绘制成如图所示的两幅不完整的统计图，根据图中所给出的信息解答下列问题：
（1）一等奖所占的比例是多少？
（2）这次数学知识竞赛获得二等奖的人数是多少？
（3）请将条形统计图补充完整；
（4）若给所有参赛学生每人发一张卡片，各自写上自己的名字，然后把卡片放入一个不透明的袋子里，摇匀后任意摸出一张，求摸出的卡片上是写有三等奖学生名字的概率．

Answer 1

分析 （1）根据扇形统计图所给数据，用1分别减去二、三等奖和纪念奖所占的百分比即可得到一等奖所占的比例；
（2）先用一等奖的人数除以它所占的百分比得到获奖总人数，然后用总人数乘以获二等奖所占的比例得到获得二等奖的人数；
（3）根据（2）计算的结果补全条形统计图；
（4）摸出的卡片上是写有三等奖学生名字的概率对应获二等奖所占的百分比．

解答 解：（1）一等奖所占的比例为1-20%-24%-46%=10%；
（2）这次数学知识竞赛获奖的总人数为20÷10%=200（人），
所以这次数学知识竞赛获得二等奖的人数为200×20%=40（人）；
（3）如图，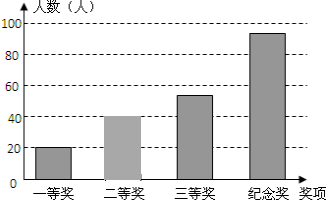

（4）摸出的卡片上是写有三等奖学生名字的概率为24%=$\frac{6}{25}$．

点评 本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．也考查了统计图和概率公式．