
分析 根据三角形的面积等于两直角边积的一半,再利用已知两直角边长,用勾股定理求斜边,得出三角形的周长.
解答 解:直角三角形的斜边长为:$\sqrt{(\sqrt{6}-\sqrt{2})^{2}+(\sqrt{6}+\sqrt{2})^{2}}$=2$\sqrt{2}$,
周长为:($\sqrt{6}$-$\sqrt{2}$)+($\sqrt{6}$+$\sqrt{2}$)+2$\sqrt{2}$=2($\sqrt{6}$+$\sqrt{2}$)(cm);
直角三角形的面积为:$\frac{1}{2}$($\sqrt{6}$-$\sqrt{2}$)×($\sqrt{6}$+$\sqrt{2}$)=2(cm2).
点评 本题考查了二次根式与三角形边长,面积的综合运用.熟练掌握勾股定理,平方差公式在计算中的作用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
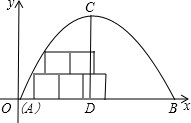 如图,某地下室横截面呈抛物线形,已知跨度AB=6m,最高点C到地面的距离CD=3m.
如图,某地下室横截面呈抛物线形,已知跨度AB=6m,最高点C到地面的距离CD=3m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com