
【题目】下面是小明设计的“作矩形ABCD”的尺规作图过程:已知:在Rt△ABC中,∠ABC=90°.求作:矩形ABCD.
作法:如图

①以点B为圆心,AC长为半径作弧;
②以点C为圆心,AB长为半径作弧;
③两弧交于点D,A,D在BC同侧;
④连接AD,CD.
所以四边形ABCD是矩形,
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:链接BD.
∵AB=________,AC=__________,BC=BC
∴ΔABC≌ΔDCB
∴∠ABC=∠DCB=90°
∴AB∥CD.
∴四边形ABCD是平行四边形
∵∠ABC=90°
∴四边形ABCD是矩形.(_______________)(填推理的依据)
【答案】(1)见解析;(2)CD,BD,有一个角是直角的平行四边形是矩形
【解析】
(1)根据作法画出对应的几何图形即可;
(2)先利用作图证明△ABC≌△DCB,得AB∥CD,根据一组对边平行且相等的四边形是平行四边形,由有一个角是直角的平行四边形是矩形可得结论.
解:(1)如图1,四边形ABCD为所作;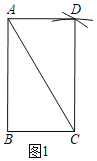
(2)完成下面的证明: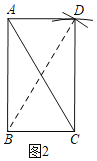
证明:如图2,连接BD.
∵AB=CD,AC=BD,BC=BC,
∴△ABC≌△DCB(SSS).
∴∠ABC=∠DCB=90°.
∴AB∥CD.
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴四边形ABCD是矩形.(有一个角是直角的平行四边形是矩形)
故答案为:CD,BD,有一个角是直角的平行四边形是矩形.


科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.
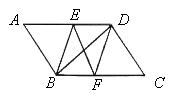
【1】△ABE≌△CDF
【2】若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一直角坐标系中,将一次函数y=x﹣3(x>1)的图象,在直线x=2(横坐标为2的所有点构成该直线)的左侧部分沿直线x=2翻折,图象的其余部分保持不变,得到一个新图象.若关于x的函数y=2x+b的图象与此图象有两个公共点,则b的取值范围是( )

A. 8>b>5B. ﹣8<b<﹣5C. ﹣8≤b≤﹣5D. ﹣8<b≤﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格线的交点叫格点,格点![]() 是
是![]() 的边
的边![]() 上的一点(请利用网格作图,保留作图痕迹).
上的一点(请利用网格作图,保留作图痕迹).

(1)过点![]() 画
画![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ;
;
(2)线段 的长度是点O到PC的距离;
(3)![]() 的理由是 ;
的理由是 ;
(4)过点C画![]() 的平行线;
的平行线;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠EAD=∠C.

(1)试判断AE与CD的位置关系,并说明理由;
(2)若∠FEC=∠BAE,∠EFC=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.

②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com