
已知:如图(1) △ABC、△ADE都是等腰直角三角形,连结BD、CE。
1.求证:△BAD≌△CAE;
2.如果△ADE绕点A逆时针旋转,恰好点C、D、E三点在同一直线上(如图(2)所示)。试猜想线段BD和CE有什么关系,并证明你的猜想。

1.证明:
∵ △ABC、△ADE都是等腰直角三角形
∴ AB=AC AD=AE
∠BAC=![]() ∠DAE=
∠DAE=![]()
∴ ∠BAC=∠DAE
∴ ∠BAC-∠DAC=∠DAE-∠DAC
即 ∠BAD=∠CAE
在△BAD和△CAE中
∵ 
∴ △BAD≌△CAE (SAS)
2.猜想:BD=CE 且BD⊥CE
证明:∵ △ABC、△ADE都是等腰直角三角形
∴ AB=AC AD=AE
∠BAC=![]() ∠DAE=
∠DAE=![]()
∴ ∠BAC=∠DAE
∴ ∠BAC+∠DAC=∠DAE+∠DAC
即 ∠BAD=∠CAE
在△BAD和△CAE中
∵ 
∴ △BAD≌△CAE (SAS)
∴ BD=CE
∵ △ADE是等腰直角三角形
∴ ∠E=![]() ∠ADE=
∠ADE=![]()
∵ △BAD≌△CAE
∴ ∠ADB=∠E=![]()
∴ ∠BDE=∠ADE+∠BDA=![]() +
+![]() =
=![]()
即BD⊥CE
∴ BD=CE且BD⊥CE
解析:略


科目:初中数学 来源: 题型:
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 3 |
2
| ||
| 3 |
| 3 |
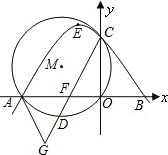 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧 |
| OA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com