
 一块矩形木板ABCD,长AD=3cm,宽AB=2cm,小虎将一块等腰直角三角板的一条直角边靠在顶点C上,另一条直角边与AB边交于点E,三角板的直角顶点P在AD边上移动(不含端点A、D),当线段BE最短时,AP的长为( )
一块矩形木板ABCD,长AD=3cm,宽AB=2cm,小虎将一块等腰直角三角板的一条直角边靠在顶点C上,另一条直角边与AB边交于点E,三角板的直角顶点P在AD边上移动(不含端点A、D),当线段BE最短时,AP的长为( )| A. | $\frac{1}{2}$cm | B. | 1cm | C. | $\frac{3}{2}$cm | D. | 2cm |
分析 设BE=y,AP=x,由△AEP∽△DPC,得$\frac{AP}{CD}$=$\frac{AE}{PD}$,构建二次函数即可解决问题.
解答  解:设BE=y,AP=x,
解:设BE=y,AP=x,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵∠EPC=90°,
∴∠APE+∠AEP=90°,∠APE+∠CPD=90°,
∴∠AEP=∠CPD,
∴△AEP∽△DPC,
∴$\frac{AP}{CD}$=$\frac{AE}{PD}$,
∴$\frac{x}{2}$=$\frac{2-y}{3-x}$,
∴y=x2-3x+4=$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{7}{8}$.
∵a=1>0,
∴x=$\frac{3}{2}$时,y有最小值,
故选C.
点评 本题考查相似三角形的判定和性质、二次函数的性质等知识,解题的关键是学会构建二次函数,解决最值问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
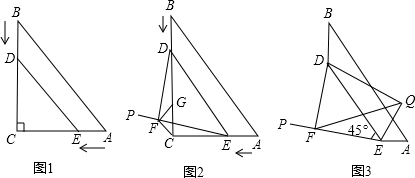
 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,PF∥BC交AB于F,连接PQ交AB于D.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,PF∥BC交AB于F,连接PQ交AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两种作物单位面积产量的比是7:8.现要把一块长150m,宽为100m的长方形土地,如图分为两块小长方形土地,左边长方形种甲种作物,右边长方形种乙种作物.怎样划分这块土地,使甲、乙两种作物的总产量相等?
甲、乙两种作物单位面积产量的比是7:8.现要把一块长150m,宽为100m的长方形土地,如图分为两块小长方形土地,左边长方形种甲种作物,右边长方形种乙种作物.怎样划分这块土地,使甲、乙两种作物的总产量相等?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,BD与AE交于点F.
如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,BD与AE交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com