
 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
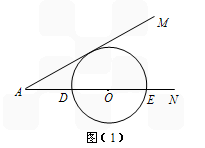
 18、已知:如图,∠MAN=45°,B为AM上的一个定点.若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C.请确定⊙P的位置,使BC恰与⊙P相切.
18、已知:如图,∠MAN=45°,B为AM上的一个定点.若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C.请确定⊙P的位置,使BC恰与⊙P相切.查看答案和解析>>
科目:初中数学 来源:2013届北京市三十一中学初三上学期期中考试数学试卷(带解析) 题型:解答题
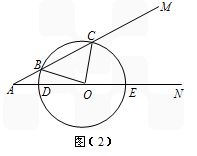
已知:如图,∠MAN=45°,B为AM上的一个定点, 若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C,请确定⊙P的位置,使BC恰与⊙P相切.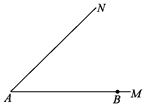
(1)画出图形(不要求尺规作图,不要求写画法);
(2)连结BP并填空:
① ∠ABC= °;
② 比较大小:∠ABP ∠CBP.(用“>”、“<”或“=”连接)
查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市初三上学期期中考试数学试卷(解析版) 题型:解答题
已知:如图,∠MAN=45°,B为AM上的一个定点, 若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C,请确定⊙P的位置,使BC恰与⊙P相切.
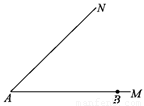
(1)画出图形(不要求尺规作图,不要求写画法);
(2)连结BP并填空:
① ∠ABC= °;
② 比较大小:∠ABP ∠CBP.(用“>”、“<”或“=”连接)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com