
 (1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点,求线段MN的长度;
(1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点,求线段MN的长度;分析 (1)由线段中点的定义可知:MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}BC$,从而可求得MN的长;
(2)由线段中点的定义解答即可.
解答 解:(1)∵点M、N分别是AC、BC的中点,
∴MC=$\frac{1}{2}AC$=2.5,NC=$\frac{1}{2}BC$=1.5.
∴MN=MC+NC=2.5+1.5=4cm.
(2)∵点M、N分别是AC、BC的中点,
∴MC=$\frac{1}{2}AC$=$\frac{1}{2}a$,NC=$\frac{1}{2}BC$=$\frac{1}{2}b$.
∴MN=MC+NC=$\frac{1}{2}a+\frac{1}{2}b$=$\frac{1}{2}(a+b)$.
点评 本题主要考查的是线段中点的定义、两点间的距离,明确线段中点的定义是解题的关键.


科目:初中数学 来源: 题型:填空题
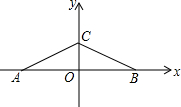 如图,在直角坐标系中,有点A(-2,0)、B(2,0)、C(0,1),另有一点D与点A、B、C构成平行四边形的顶点,则点D的坐标是(4,1),(-4,1),(0,-1).
如图,在直角坐标系中,有点A(-2,0)、B(2,0)、C(0,1),另有一点D与点A、B、C构成平行四边形的顶点,则点D的坐标是(4,1),(-4,1),(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数
如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数 ,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.
,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
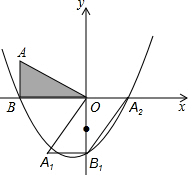 如图,AB⊥x轴于点B,AB=3,tan∠AOB=$\frac{3}{4}$,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
如图,AB⊥x轴于点B,AB=3,tan∠AOB=$\frac{3}{4}$,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
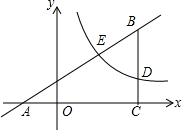 如图,在直角坐标系中,Rt△ABC的边AC在x轴上,tanA=$\frac{1}{2}$,∠ACB=90°,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象与BC边交于点D,与AB边交于点E,点D,E的横坐标分别为4,2.△BDE的面积为2.
如图,在直角坐标系中,Rt△ABC的边AC在x轴上,tanA=$\frac{1}{2}$,∠ACB=90°,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象与BC边交于点D,与AB边交于点E,点D,E的横坐标分别为4,2.△BDE的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
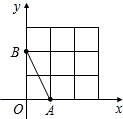 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com