Question

5．在如图的直角坐标系中，已知点A（1，0）、B（0，-2），将线段AB绕点A按逆时针方向旋转90°至AC，若抛物线y=-$\frac{1}{2}$x²+bx+2经过点C．
（1）求抛物线的解析式；
（2）如图，将抛物线平移，当顶点至原点时，过Q（0，-2）作不平行于x轴的直线交抛物线于E、F两点，问在y轴的正半轴上是否存在一点P，使△PEF的内心在y轴上？若存在，求出点P的坐标；若不存在，说明理由．
（3）在抛物线上是否存在一点M，使得以M为圆心，以$\frac{\sqrt{10}}{2}$为半径的圆与直线BC相切？若存在，请求出点M的坐标；若不存在，请说明理由．

Answer 1

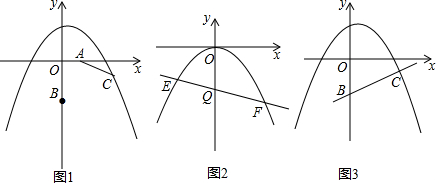
分析 （1）根据题意得出△AOB≌△CDA，从而求得OA=CD=1，AD=OB=2，即可求得C的坐标，然后把C的坐标代入抛物线的解析式即可求得b；
（2）将抛物线平移，当顶点至原点时，解析式为y=-$\frac{1}{2}$x²，设EF的解析式为y=kx-2（k≠0）．假设存在满足题设条件的点P（0，t），过P作GH∥x轴，分别过E，F作GH的垂线，垂足为G，H．由△PEF的内心在y轴上，得出∠GEP=∠EPQ=∠QPF=∠HFP，那么△GEP∽△HFP，根据相似三角形对应边成比例以及根与系数的关系即可求解；
（3）根据B、C坐标根据待定系数法求得解析式，求得直线与x轴的解得坐标，在y轴上去一点K，作KS⊥BC于S，使KS=$\frac{\sqrt{10}}{2}$，易证得△BOG∽△BSK，由对应边成比例求得BK的出，既然求得K的坐标，过K点作BC平行线交抛物线的交点即为M点，求得平行线的解析式，然后和抛物线的解析式联立方程即可求得．

解答 解：（1）如图1，∵点A（1，0）、B（0，-2），将线段AB绕点A按逆时针方向旋转90°至AC，
∴AB=AC，
连接AB，作CD⊥OD于D，
∵△AOB≌△CDA，
∴OA=CD，AD=OB，
∴C（3，-1），
∵抛物线y=-$\frac{1}{2}$x²+bx+2经过点C．
∴-1=-$\frac{1}{2}$×9+3b+2，解得b=$\frac{1}{2}$，
∴抛物线的解析式为y=-$\frac{1}{2}$x²+$\frac{1}{2}$x+2；
（2）将抛物线平移，当顶点至原点时，抛物线为y=-$\frac{1}{2}$x²，
设EF的解析式为y=kx-2（k≠0）．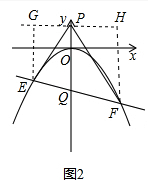
假设存在满足题设条件的点P（0，t），
如图2，过P作GH∥x轴，分别过E，F作GH的垂线，垂足为G，H．
∵△PEF的内心在y轴上，
∴∠GEP=∠EPQ=∠QPF=∠HFP，
∴△GEP∽△HFP，
∴GP：PH=GE：HF，
∴-x_E：x_F=（t-y_E）：（t-y_F）=（t-kx_E+2）：（t-kx_F+2），
∴2kx_E•x_F=（t+2）（x_E+x_F），
 由y=-$\frac{1}{2}$x²，y=kx-2，得x²+2kx-4=0，
∴x_E+x_F=-2k，x_E•x_F=-4，
∴2k（-4）=（t+2）•（-2k），
∵k≠0，∴t=2，
∴y轴的正半轴上存在点P（0，2），使△PEF的内心在y轴上；
（3）∵B（0，-2），C（3，-1），
设直线BC的解析式为y=mx-2，
∴-1=3m-2，
∴m=$\frac{1}{3}$，
∴y=$\frac{1}{3}$x-2，
∴直线BC与x轴的交点G（6，0），
∴OB=2，OG=6，
∴BG=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$，
在y轴上去一点K，作KS⊥BC于S，使KS=$\frac{\sqrt{10}}{2}$，
∵∠BOG=∠BSK=90°，∠OBG=∠SBK，
∴△BOG∽△BSK，
∴$\frac{BK}{BG}$=$\frac{KS}{OG}$，即$\frac{BK}{2\sqrt{10}}$=$\frac{\frac{\sqrt{10}}{2}}{6}$，
∴BK=$\frac{5}{3}$，
∴OK=$\frac{1}{3}$或$\frac{11}{3}$，
∴K（0，-$\frac{1}{3}$）或（0，-$\frac{11}{3}$）
作KM∥BC交抛物线与M，
∴直线KM为y=$\frac{1}{3}$x-$\frac{1}{3}$或y=$\frac{1}{3}$x-$\frac{11}{3}$，
解$\left\{\begin{array}{l}{y=\frac{1}{3}x-\frac{1}{3}}\\{y=-\frac{1}{2}{x}^{2}+\frac{1}{2}x+2}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=-1}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=\frac{7}{3}}\\{{y}_{2}=\frac{4}{9}}\end{array}\right.$，
解$\left\{\begin{array}{l}{y=\frac{1}{3}x-\frac{11}{3}}\\{y=-\frac{1}{2}{x}^{2}+\frac{1}{2}x+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1+\sqrt{409}}{6}}\\{y=-\frac{5-\sqrt{409}}{18}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1-\sqrt{409}}{6}}\\{y=-\frac{5+\sqrt{409}}{18}}\end{array}\right.$，
∴在抛物线上是否存在一点M，使得以M为圆心，以$\frac{\sqrt{10}}{2}$为半径的圆与直线BC相切，点M的坐标为（-2，-1）或（$\frac{7}{3}$，$\frac{4}{9}$）或（$\frac{1+\sqrt{409}}{6}$，-$\frac{5-\sqrt{409}}{18}$）或（$\frac{1-\sqrt{409}}{6}$，-$\frac{5+\sqrt{409}}{18}$）．

点评 本题是二次函数综合题，其中涉及到利用待定系数法求抛物线的解析式，二次函数平移的规律，一次函数与二次函数的交点，三角形的内心，相似三角形的判定与性质等知识．综合性较强，有一定难度．利用数形结合与方程思想是解题的关键．