
【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
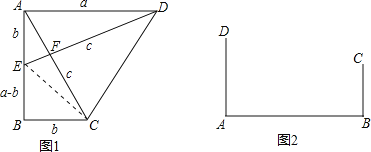
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式![]() 最小值(0<x<16)
最小值(0<x<16)
【答案】【小试牛刀】![]() ,
,![]() ,
,![]() ,
,![]() a(a+b)=
a(a+b)=![]() b(a-b)+
b(a-b)+![]() c2.
c2.
【知识运用】(1)41;(2)作图见解析;
【知识迁移】20.
【解析】
【小试牛刀】
根据三角形的面积和梯形的面积就可表示出.
【知识运用】
(1)连接CD,作CE⊥AD于点E,根据AD⊥AB,BC⊥AB得到BC=AE,CE=AB,从而得到DE=AD-AE=24-16=8千米,利用勾股定理求得CD两地之间的距离.
(2)连接CD,作CD的垂直平分线角AB于P,P即为所求;设AP=x千米,则BP=(40-x)千米,分别在Rt△APD和Rt△BPC中,利用勾股定理表示出CP和PD,然后通过PC=PD建立方程,解方程即可.
【知识迁移】
根据轴对称-最短路线的求法即可求出.
[小试牛刀]
S梯形ABCD=![]()
S△EBC=![]()
S四边形AECD=![]() .
.
根据S梯形ABCD= S△EBC + S四边形AECD,得![]() a(a+b)=
a(a+b)=![]() b(a-b)+
b(a-b)+![]() c2.
c2.
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() a(a+b)=
a(a+b)=![]() b(a-b)+
b(a-b)+![]() c2.
c2.
[知识运用](1)如图2①,连接CD,作CE⊥AD于点E,
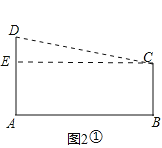
∵AD⊥AB,BC⊥AB,
∴BC=AE,CE=AB,
∴DE=AD-AE=25-16=9千米,
∴CD=![]() =41千米,
=41千米,
∴两个村庄相距41千米.
故答案为41.
(2)如图2②所示:
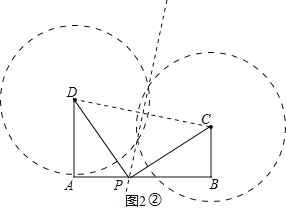
设AP=x千米,则BP=(40-x)千米,
在Rt△ADP中,DP2=AP2+AD2=x2+242,
在Rt△BPC中,CP2=BP2+BC2=(40-x)2+162,
∵PC=PD,
∴x2+242=(40-x)2+162,
解得x=16,
即AP=16千米.
[知识迁移]:如图3,
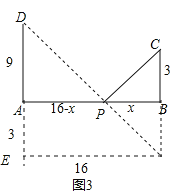
代数式![]() 的最小值为:
的最小值为:![]() =20.
=20.


科目:初中数学 来源: 题型:
【题目】如图,在山顶上有一座电视塔,在塔顶B处,测得地面上一点A的俯角α=60°,在塔底C处测得的俯角β=45°,已知BC=60m,求山高CD(精确到1m, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(不写作法,但必须保留作图痕迹)
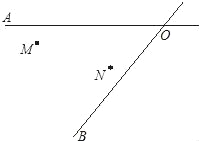
如图:某地有两所大学和两条相交叉的公路,(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库P应该建在什么位置吗?在所给的图形中画出你的设计方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB为半圆O的直径,C为圆上一点,AD平分∠BAC交半圆于点D,过点D作DE⊥AC,DE交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,DE= ![]() ,求线段AC的长
,求线段AC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:① x + y=a;② x-y=b;③ a2-b2=2xy;④ x2-y2=ab;⑤ x2 + y2=![]() ,其中正确的有__________.
,其中正确的有__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.
(1)几秒后P、Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1 , △ABC的面积为S2 , 在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
![]() 若
若![]() ,求线段MN的长;
,求线段MN的长;
![]() 若C为线段AB上任一点,满足
若C为线段AB上任一点,满足![]() ,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
![]() 若C在线段AB的延长线上,且满足
若C在线段AB的延长线上,且满足![]() cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com