
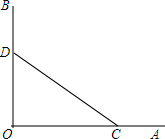
 画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.分析 (1)利用基本作图(作一个角的平分线)作OP平分∠AOB,再作线段CD的垂直平分线,从而可得到OE、CF、DF;
(2)根据线段垂直平分线的性质得到FD=FC,AE=CE,然后根据直角三角形斜边上的中线性质得到OE=$\frac{1}{2}$CD.
解答 解:(1)如图,OE、CF、DF为所作;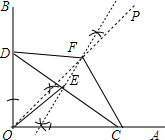
(2)OE=$\frac{1}{2}$CD,DF=CF.理由如下:
∵EF垂直平分CD,
∴FD=FC,AE=CE,
而∠AOB=90°,
∴OE为Rt△OCD斜边上的中线,
∴OE=$\frac{1}{2}$CD.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠D=40°,∠E=80°,∠A=60°,∠B=80° | |
| B. | ∠A=∠D,AB:AC=DF:EF | |
| C. | ∠B=∠E=90°,BC:EF=AC:DF | |
| D. | AB=1,BC=2,CA=1.5,DE=6,EF=4,FD=8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有一块长为30m,宽为20m的矩形菜地,准备修筑同样宽的三条直路(如图),把菜地分成六块作为试验田,种植不同品种的蔬菜,并且种植蔬菜面积为矩形菜地面积的$\frac{3}{4}$,设道路的宽度为x m,下列方程:
有一块长为30m,宽为20m的矩形菜地,准备修筑同样宽的三条直路(如图),把菜地分成六块作为试验田,种植不同品种的蔬菜,并且种植蔬菜面积为矩形菜地面积的$\frac{3}{4}$,设道路的宽度为x m,下列方程:| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
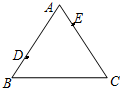 如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似.
如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com