
分析 先根据直角三角形两锐角互余得出∠A+∠B=90°,又∠A=2∠B,求∠B=30°,再利用含30度角的直角三角形的性质得出AB=2AC,BC=$\sqrt{3}$AC,进而求出AC:BC.
解答 解:∵在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°,
∵∠A=2∠B,
∴∠A=60°,∠B=30°,
∴AB=2AC,BC=$\sqrt{3}$AC,
∴AC:BC=1:$\sqrt{3}$=$\frac{\sqrt{3}}{3}$.
故答案为$\frac{\sqrt{3}}{3}$.
点评 本题考查了含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.也考查了直角三角形两锐角互余的性质,求出∠B=30°是解题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
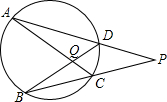 如图,直线PB、PA分别交圆于C、B,D、A,AC、BD交于Q,若$\widehat{AB}$:$\widehat{DC}$=3:1,∠AQB=α,求∠P.
如图,直线PB、PA分别交圆于C、B,D、A,AC、BD交于Q,若$\widehat{AB}$:$\widehat{DC}$=3:1,∠AQB=α,求∠P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
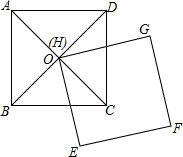 如图,已知正方形ABCD的中心为O,用纸片剪下一个大小与正方形ABCD相等的正方形EFGH,然后把正方形EFGH的顶点H固定在点O,让正方形EFGH绕点O旋转,正方形ABCD与纸片重合的部分随着纸片旋转的位置不同,而形状也会有所改变,它们有什么相同的地方吗?请你探究问题的结论
如图,已知正方形ABCD的中心为O,用纸片剪下一个大小与正方形ABCD相等的正方形EFGH,然后把正方形EFGH的顶点H固定在点O,让正方形EFGH绕点O旋转,正方形ABCD与纸片重合的部分随着纸片旋转的位置不同,而形状也会有所改变,它们有什么相同的地方吗?请你探究问题的结论查看答案和解析>>
科目:初中数学 来源: 题型:解答题
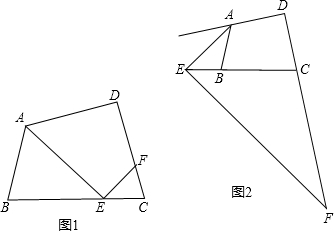
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A | 2 | 3 | 4 | 5 | 6 | … | 2009 |
| B | 1 | 2 | 3 | 4 | 5 | … | 2008 |
| C | 1 | 4 | 7 | 10 | 13 | … | x |
| A. | 2007 | B. | 4017 | C. | 6022 | D. | 6025 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com