
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 1,1,$\sqrt{3}$ | C. | 4,5,6 | D. | 1,$\sqrt{3}$,2 |
分析 根据勾股定理的逆定理对各选项进行逐一分析即可.
解答 解:A、∵($\sqrt{3}$)2+($\sqrt{4}$)2≠($\sqrt{5}$)2,∴此组数据不能作为直角三角形的三边长,故本选项错误;
B、∵12+12=2≠($\sqrt{3}$)2,∴此组数据不能作为直角三角形的三边长,故本选项错误;
C、∵42+52=41≠62,∴此组数据不能作为直角三角形的三边长,故本选项错误;
D、∵12+($\sqrt{3}$)2=4=22,∴此组数据能作为直角三角形的三边长,故本选项正确.
故选D.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a=1,b=2 | B. | a=-1,b=2 | C. | a=-1,b=-2 | D. | a=1,b=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25000名考生是总体 | B. | 每名考生的成绩是个体 | ||
| C. | 1000名考生是总体的一个样本 | D. | 样本容量是25000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
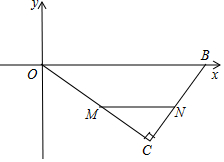 已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.
已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若am>bm,则a>b | B. | 若am2>bm2,则a>b | ||
| C. | 若a>b,则am2>bm2 | D. | 若a>b且ab>0,则$\frac{1}{a}$>$\frac{1}{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com