
 已知,如图,在△ABC中,∠ACB=90°,点D在AB上,CD=CB,求作:∠A=$\frac{1}{2}$∠BCD.
已知,如图,在△ABC中,∠ACB=90°,点D在AB上,CD=CB,求作:∠A=$\frac{1}{2}$∠BCD. 分析 根据直角三角形的性质得到∠B=90°-∠A,由等腰三角形的性质得到∠B=∠BDC,求得∠B=$\frac{1}{2}$(180°-∠BCD),于是得到90°-∠A=$\frac{1}{2}$(180°-∠BCD),即可得到结论.
解答 解:在△ABC中,∵∠ACB=90°,
∴∠B=90°-∠A,
∵CD=CB,
∴∠B=∠BDC,
∴∠B=$\frac{1}{2}$(180°-∠BCD),
∴90°-∠A=$\frac{1}{2}$(180°-∠BCD),
∴∠A=$\frac{1}{2}$∠BCD.
点评 本题考查了等腰三角形的性质,直角三角形的性质,熟练掌握等腰三角形的性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
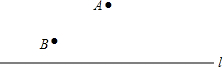 如图,体育课上,老师正在组织学生做游戏,要求同学们单手拍球从A处出发,到达直线l后立即向B处,到达B处用时最少的同学获胜,请你为同学们设计一条最短的运动路线,使同学们的用时尽量能少.
如图,体育课上,老师正在组织学生做游戏,要求同学们单手拍球从A处出发,到达直线l后立即向B处,到达B处用时最少的同学获胜,请你为同学们设计一条最短的运动路线,使同学们的用时尽量能少.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -x3+y5 | B. | 2x2-3 | C. | abc-1 | D. | a2+2ab+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com