
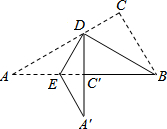
 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | $\frac{10}{3}$ |
分析 根据直角三角形两锐角互余求出∠ABC=60°,翻折前后两个图形能够互相重合可得∠BDC=∠BDC′,∠CBD=∠ABD=30°,∠ADE=∠A′DE,然后求出∠BDE=90°,再解直角三角形求出BD,然后求出DE即可.
解答  解:∵△ABC是直角三角形,∠A=30°,
解:∵△ABC是直角三角形,∠A=30°,
∴∠ABC=90°-30°=60°,
∵将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,
∴∠BDC=∠BDC′,∠CBD=∠ABD=$\frac{1}{2}$∠ABC=30°,
∵沿DE折叠点A落在DC′的延长线上的点A′处,
∴∠ADE=∠A′DE,
∴∠BDE=∠ABD+∠A′DE=$\frac{1}{2}$×180°=90°,
在Rt△BCD中,BD=BC÷cos30°=5÷$\frac{\sqrt{3}}{2}$=$\frac{10\sqrt{3}}{3}$cm,
在Rt△BDE中,DE=BD•tan30°=$\frac{10\sqrt{3}}{3}$×$\frac{\sqrt{3}}{3}$=$\frac{10}{3}$cm.
故选:D.
点评 本题考查了翻折变换的性质,解直角三角形,熟记性质并分别求出有一个角是30°角的直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
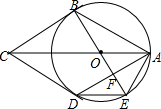 如图,AB,AD是⊙O的弦,AO平分∠BAD.过点B作⊙O的切线交AO的延长线于点C,连接CD,BO.延长BO交⊙O于点E,交AD于点F,连接AE,DE.
如图,AB,AD是⊙O的弦,AO平分∠BAD.过点B作⊙O的切线交AO的延长线于点C,连接CD,BO.延长BO交⊙O于点E,交AD于点F,连接AE,DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1+(1-x)=1 | B. | 1-(1-x)=1 | C. | 1+(1-x)=x-3 | D. | 1-(1-x)=x-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.488×104 | B. | 0.1488×107 | C. | 14.88×106 | D. | 1.488×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
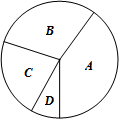 学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:| 类别 | A | B | C | D |
| 频数 | 20 | m | 11 | 4 |
| 频率 | n | 0.3 | 0.22 | 0.08 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com