

分析 (1)利用待定系数法求二次函数的解析式;
(2)有三种情况:分别以BC为腰和底边进行分类讨论:
①以B为圆心以BC为半径画圆交对称轴于D1和D2;
②以BC为底边时,作BC的中垂线交对称轴于D3;
分别计算点D的坐标即可;
(3)先计算直线BC的解析式:y=x-3,表示P(t,t-3),M(t,t2-2t-3),
分情况进行讨论:
①当0<t<3时,即点P在线段BC上时,如图4,
②当t>3时,如图5,
③当t<0时,如图6,
分别表示PM和QH的长,代入三角形面积公式计算即可.
解答 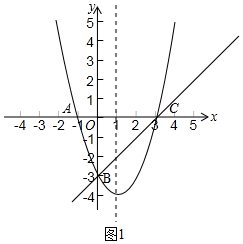 解:(1)如图1,把A(-1,0),B(0,-3)代入y=x2+bx+c中得:
解:(1)如图1,把A(-1,0),B(0,-3)代入y=x2+bx+c中得:
$\left\{\begin{array}{l}{1-b+c=0}\\{c=-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$
∴这个抛物线的解析式为:y=x2-2x-3;
(2)如图2,当BC=BD1时,过D1作D1M⊥y轴于M,
∴D1M=1,
由对称性得:C(3,0),
∴OC=3,
∴BD1=BC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
Rt△BMD1中,BM=$\sqrt{(3\sqrt{2})^{2}-{1}^{2}}$=$\sqrt{17}$,
∴MO=$\sqrt{17}$-3,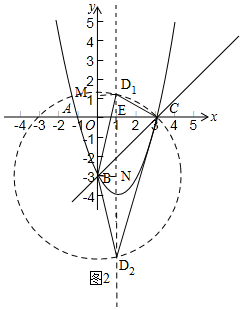
∴D1(1,$\sqrt{17}$-3);
当BD2=BC时,过B作BN⊥D1D2于N,
同理得:D2N=$\sqrt{17}$,
∴ED2=$\sqrt{17}$+3,
∴D2(1,-$\sqrt{17}$-3);
如图3,作BC的中垂线交对称轴于D3,连接D3B、D3C,
∴D3B=D3C,
∴∠D3BC=∠D3CB,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBD3=∠OCD3,
过D3作D3F⊥y轴于F,
易得△D3FB≌△D3EC,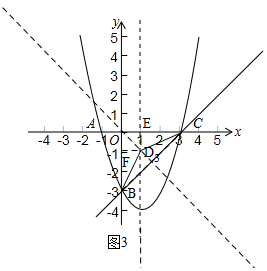
∴D3E=D3F=1,
∴D3(1,-1);
综上所述,点D的坐标为:(1,$\sqrt{17}$-3)或(1,-$\sqrt{17}$-3)或(1,-1);
(3)设直线BC的解析式为:y=kx+b,
把B(0,-3)和C(3,0)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴直线BC的解析式为:y=x-3,
如图4,过Q作QH⊥PM于H,
∵△OBC是等腰直角三角形,
∴∠OCB=45°,
∴△PEC是等腰直角三角形,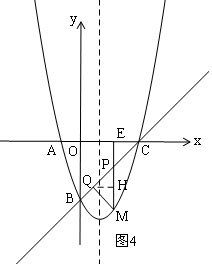
∴∠EPC=∠QPH=45°,
∴△QPH是等腰直角三角形,
∵PQ=$\sqrt{2}$,
∴QH=PH=1,
∵P(t,t-3),M(t,t2-2t-3),
当0<t<3时,即点P在线段BC上时,如图4,
PM=t-3-(t2-2t-3)=-t2+3t,
∴S△PQM=S=$\frac{1}{2}$PM•QH=$\frac{1}{2}$(-t2+3t)×1=-$\frac{1}{2}{t}^{2}$+$\frac{3}{2}$t,
当t>3时,如图5,
QH=1,PM=t2-2t-3-(t-3)=t2-3t,
∴S△PQM=S=$\frac{1}{2}$PM•QH=$\frac{1}{2}$(t2-3t)×1=$\frac{1}{2}{t}^{2}$-$\frac{3}{2}$t,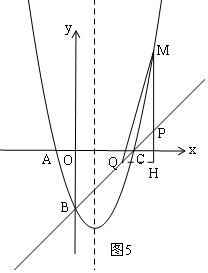
当t<0时,如图6,
QH=1,PM=t2-2t-3+(-t+3)=t2-3t,
∴S△PQM=S=$\frac{1}{2}$PM•QH=$\frac{1}{2}$(t2-3t)×1=$\frac{1}{2}{t}^{2}$-$\frac{3}{2}$t;
综上所述,S与t之间的函数关系式为:$\left\{\begin{array}{l}{-\frac{1}{2}{t}^{2}+\frac{3}{2}t(0<t<3)}\\{\frac{1}{2}{t}^{2}-\frac{3}{2}t(t<0或t>3)}\end{array}\right.$.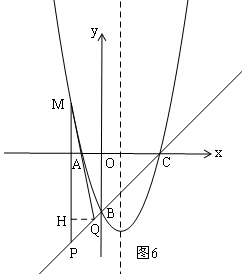
点评 本题是二次函数的综合题,考查了利用待定系数法求函数的解析式、等腰三角形与等腰直角三角形的判定和性质,本题的2、3问采用了分类讨论的思想解决问题,此类问题容易丢解,要考虑完全,是一道不错的二次函数压轴题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:选择题
| A. | 275×104 | B. | 2.75×104 | C. | 2.75×1012 | D. | 27.5×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某化妆公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售费中提取一定数量的费用):
某化妆公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售费中提取一定数量的费用):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
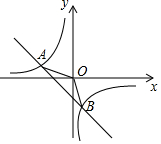 如图,一次函数y=ax+b(a,b为常数,并且a≠0)的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交相交于点A(-2,1),B(1,n)
如图,一次函数y=ax+b(a,b为常数,并且a≠0)的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交相交于点A(-2,1),B(1,n)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com