
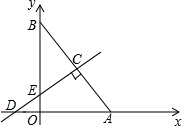
 ��ͼ����ƽ��ֱ������ϵ�У���֪Rt��AOB����ֱ�DZ�OA��OB�ֱ���x�ᣬy����������ϣ���A��6��0����cos��BAO=$\frac{3}{5}$���߶�AB�Ĵ�ֱƽ����CD��AB�ڵ�C����y���ڵ�E����x���ڵ�D��
��ͼ����ƽ��ֱ������ϵ�У���֪Rt��AOB����ֱ�DZ�OA��OB�ֱ���x�ᣬy����������ϣ���A��6��0����cos��BAO=$\frac{3}{5}$���߶�AB�Ĵ�ֱƽ����CD��AB�ڵ�C����y���ڵ�E����x���ڵ�D������ ��1����������Ǻ����������ֵ��
��2��������������λ�ߵ�������õ�C�����꣬�����ֱ��AB�Ľ���ʽ����CD��ֱƽ��AB���õ�ֱ��CD��б�ʣ��������CD�Ľ���ʽ��
��3����Ϊ��PΪֱ��CD��һ�㣬��CP=$\frac{1}{2}$AB��֤�����������ĵ�P���������ٸ��ݵ�C��P��M���п�����ֱ�Ƕ��㣬�������ۣ�������������ĵ�M�ĸ�����
��� �⣺��1����A��6��0����OA=6��
��cos��BAO=$\frac{3}{5}$��
��AB=$\frac{OA}{\frac{3}{5}}$=$\frac{6}{\frac{3}{5}}$=10��
��OB=$\sqrt{{AB}^{2}{-OA}^{2}}$=8��
��B��0��8����
��tan��BAO=$\frac{OB}{OA}$=$\frac{4}{3}$��
��2����CD��ֱƽ��AB��
��C��3��4����
��ֱ��AB�Ľ���ʽΪ��y=kx+b��
��$\left\{\begin{array}{l}{0=6k+b}\\{8=b}\end{array}\right.$����$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=8}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪ��y=-$\frac{4}{3}$x+8��
��CD��AB��
����ֱ��CD�Ľ���ʽΪ��y=$\frac{3}{4}$x+m��
��4=$\frac{3}{4}$��3+m��
��m=$\frac{7}{4}$��
��ֱ��CD�Ľ���ʽΪ��y=$\frac{3}{4}$x+$\frac{7}{4}$��
��3���ߵ�PΪֱ��CD��һ�㣬��CP=$\frac{1}{2}$AB��
�����������ĵ�P��������
����PCM=90�㣬PC=MCʱ����M���A���B�غϣ�
�������ĵ�M��2����
����CPM=90�㣬PM=PC��
�������ĵ�M��4����
����CMP=90�㣬CM=PMʱ��
�������ĵ�M��4����
���Ե�C��P��MΪ������������ǵ���ֱ�������Σ����������ĵ�M�ĸ�����10��
���� ���⿼����������Ǻ����Ķ��壬���ɶ�����Ӧ�ã�����ϵ���������Ľ���ʽ������ֱ�������ε��ж���Ҫע����ǣ�3���У�Ҫ����M��IJ�ͬλ�ý��з�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
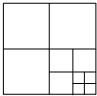 ��ͼ����һ��������ֽƬ�����ĸ�С�����Σ�Ȼ�����е�һ���������ټ����ĸ�С�����Σ��ٽ����е�һ�������μ����ĸ�С�����Σ���˼�����ȥ����������������ϲ��������õ��������εĸ����Ĺ�����ɸ��⣮
��ͼ����һ��������ֽƬ�����ĸ�С�����Σ�Ȼ�����е�һ���������ټ����ĸ�С�����Σ��ٽ����е�һ�������μ����ĸ�С�����Σ���˼�����ȥ����������������ϲ��������õ��������εĸ����Ĺ�����ɸ��⣮| ��������N | 1 | 2 | 3 | 4 | 5 | �� | n |
| ������� | 4 | 7 | 10 | an |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
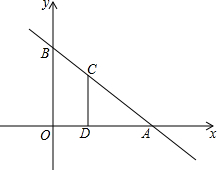 ��ͼ��ƽ��ֱ������ϵ�У�ֱ��AB��y=-$\frac{3}{4}$x+3��x�ᡢy��ֱ���A��4��0����B��0��3�����㣬��CΪ�߶�AB�ϵ�һ���㣬����C��CD��x����D��
��ͼ��ƽ��ֱ������ϵ�У�ֱ��AB��y=-$\frac{3}{4}$x+3��x�ᡢy��ֱ���A��4��0����B��0��3�����㣬��CΪ�߶�AB�ϵ�һ���㣬����C��CD��x����D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �û�ÿ����ˮ�� | ����ˮ���ۣ�Ԫ/�֣� | ��ˮ�������ã�Ԫ/�֣� |
| 17�ּ����� | a | 0.80 |
| ����17�ֲ�����30�ֵIJ��� | b | 0.80 |
| ����30�ֵIJ��� | 6.00 | 0.80 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com