
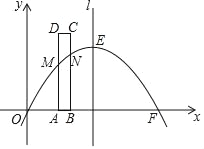
����Ŀ�������ģ���ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��l��������![]() �ཻ��A��1��
�ཻ��A��1��![]() ����B��4��0�����㣮
����B��4��0�����㣮

��1����������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�D��ʹ�á�ABD�����߶�ABΪб�ߵ�ֱ�������Σ������ڣ������D�����ꣻ�������ڣ�˵�����ɣ�
��3����P���߶�AB��һ���㣬����P�����A��B�غϣ�������P��PM��OA������һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������BCN����PMN�����S��BCN��S��PMN����S��BCN=2S��PMN�����![]() ��ֵ���������ʱ��M�����꣮
��ֵ���������ʱ��M�����꣮
���𰸡���1��![]() ����2��D��1��0����0��
����2��D��1��0����0��![]() ����0��
����0��![]() ������3��
������3��![]() ��M��
��M��![]() ��
��![]() ����
����
��������
��1����A��B��������꣬���ô���ϵ��������������߽���ʽ��
��2����D��x���Ϻ�y���ϣ���D��x����ʱ����A��AD��x�ᣬ����D��Ϊ����D����y����ʱ�����D������Ϊ��0��d�����ɷֱ��ʾ��AD��BD�������ù��ɶ����ɵõ�����d�ķ��̣������d��ֵ���Ӷ����������������D�����ꣻ
��3����P��PF��CM�ڵ�F������Rt��ADO��Rt��MFP�Լ����Ǻ���������PF�ֱ��ʾ��MF��NF���Ӷ��ɱ�ʾ��MN����BC=a�������a��ʾ��CN��������S��BCN=2S��PMN������PF��ʾ��a��ֵ���Ӷ�����PF��ʾ��CN�������![]() ��ֵ������a�ɱ�ʾ��M������꣬���������߽���ʽ�����a��ֵ���Ӷ������M������꣮
��ֵ������a�ɱ�ʾ��M������꣬���������߽���ʽ�����a��ֵ���Ӷ������M������꣮
��1����A��1��![]() ����B��4��0����������
����B��4��0����������![]() ��ͼ���ϣ���
��ͼ���ϣ���![]() �����
�����![]() ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2�������������������⣬�������£�
�ٵ���D��x����ʱ����ͼ1������A��AD��x���ڵ�D����A��1��![]() ����
����
��D������1��0����
�ڵ���D��y����ʱ����D��0��d����
��![]() ��
��![]() ��
��
��![]() ��
��
�ߡ�ABD����ABΪб�ߵ�ֱ�������Σ���
![]() ����
����![]() ��
��
���d=![]() ����D��������0��
����D��������0��![]() ����0��
����0��![]() ����
����
���Ͽ�֪��������������D�㣬������Ϊ��1��0����0��![]() ����0��
����0��![]() ����
����
��3����ͼ2����P��PF��CM�ڵ�F��
��PM��OA����Rt��ADO��Rt��MFP��
��![]() =
=![]() ����MF=
����MF=![]() PF��
PF��
��Rt��ABD��BD=3��AD=![]() ��
��
��tan��ABD=![]() �����ABD=60�㣬
�����ABD=60�㣬
��BC=a����CN=![]() a��
a��
��Rt��PFN�У���PNF=��BNC=30�㣬
��tan��PNF=![]() ��
��
��FN=![]() PF����MN=MF+FN=
PF����MN=MF+FN=![]() PF��
PF��
��S��BCN=2S��PMN��
��![]() ��
��
��a=![]() PF��
PF��
��NC=![]() a=
a=![]() PF��
PF��
��![]() =
=![]() =
=![]() ��
��
��MN=![]() NC=
NC=![]() =
=![]() a��
a��
��MC=MN+NC=��![]() ��a��
��a��
��M��������4��a����![]() ��a����
��a����
��M�����������ϣ�����ɵ�![]() =��
=��![]() ��a�����a=
��a�����a=![]() ��a=0����ȥ����OC=4��a=
��a=0����ȥ����OC=4��a=![]() ��MC=
��MC=![]() ��
��
���M��������![]() ��
��![]() ����
����


 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx��x��ֱ���ԭ��O�͵�F��10��0������Գ���l���ڵ�E��5��5��������ABCD�ı�AB��x���������ϣ���AB=1����AD��BC�������߷ֱ��ڵ�M��N��������ABCD��x��������ƽ�ƣ���M��Nλ�ڶԳ���l��ͬ��ʱ������MN����ʱ���ı���ABNM�������ΪS����M��Nλ�ڶԳ���l������ʱ������EM��EN����ʱ�����ABNEM�������ΪS������A���O�غϵ�λ����Ϊ����ABCDƽ�Ƶ���㣬�����ABCDƽ�Ƶij���Ϊt��0��t��5����
��1��������������ߵı���ʽ��
��2����t=0ʱ����S��OBN��ֵ��
��3��������ABCD����x���������ƽ��ʱ����S����t��0��t��5���ĺ�������ʽ�������tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�Ƽ�С�����Ұ�⿼��,Ϊ�˰�ȫ��ͨ��һƬʪ��,��������ǰ��·���������ɿ�ľ��,������һ����ʱ��·.ľ��Ե����ѹǿp(Pa)�ǹ���ľ�����S(m2)�ķ���������,��ͼ����ͼ��ʾ.
(1)��ֱ��д��p����S�ĺ�������ʽ;
(2)��ľ�����Ϊ0.2 m2ʱ,ѹǿ�Ƕ���Pa?
(3)���Ҫ��ѹǿ������6000 Pa,ľ�����������Ƕ���?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
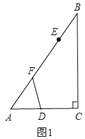
����Ŀ����ͼ(1)����Rt��ABC�У���BAC=90�㣬AD��BC�ڵ�D����O��AC���ϵ�һ�㣬����BO��AD�ڵ�F��OE��OB��BC���ڵ�E��
(1)��˵������ABF�ס�COE��
(2)��ͼ(2)����OΪAC�ߵ��е㣬��![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
(3)��OΪAC�ߵ��е㣬![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��k��0���뷴��������![]() ��ͼ���ཻ��A��B���㣬һ�κ�����ͼ����y���ཻ�ڵ�C����֪��A��4��1��
��ͼ���ཻ��A��B���㣬һ�κ�����ͼ����y���ཻ�ڵ�C����֪��A��4��1��

��1�����������Ľ���ʽ��
��2������OB��O������ԭ�㣩������BOC�����Ϊ3�����һ�κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ������
������![]() ���
���![]() �����˶���ͬʱ��
�����˶���ͬʱ��![]() ��
��![]() ������
������![]() ���
���![]() �����˶������ǵ��ٶ���ͬ����
�����˶������ǵ��ٶ���ͬ����![]() ��
��![]() �ϣ�
�ϣ�![]() ���ҵ�
���ҵ�![]() �ڵ�
�ڵ�![]() ���·�������
���·�������![]() �����
�����![]() ʱ����
ʱ����![]() ��
��![]() Ҳֹͣ�˶�������
Ҳֹͣ�˶�������![]() ����
����![]() ������������⣺
������������⣺
![]() ��ͼ
��ͼ![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
![]() ��ͼ
��ͼ![]() ����
����![]() ��
��![]() ���ۣ�ʹ��
���ۣ�ʹ��![]() ����
����![]() �㣮
�㣮
����![]() Ϊ��ֵʱ���ı���
Ϊ��ֵʱ���ı���![]() Ϊ���Σ���������ε������
�����������������
����ͼ![]() ���ֱ�ȡ
���ֱ�ȡ![]() ��
��![]() ���е�
���е�![]() ��
��![]() ���������˶������У����߶�
���������˶������У����߶�![]() ɨ�����������״Ϊ________�������Ϊ________��
ɨ�����������״Ϊ________�������Ϊ________��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У��Խ���
�У��Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() ��һ��ֱ�߷ֱ�
��һ��ֱ�߷ֱ�![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��![]() ������
������![]() ��
��![]() ��
��
![]() ��֤���ı���
��֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����AB=7cm��AC��AB��BD��AB ����ֱ�Ϊ A��B��AC=5cm����P ���߶� AB ���� 2cm/s ���ٶ��ɵ� A ���B �˶���ͬʱ���� Q ������ BD ���˶��������� ����ʱ��Ϊ t��s�������� P �˶�����ʱ���� Q �˶���֮��������

��1������ Q ���˶��ٶ���� P ���˶��ٶ���ȣ��� t=1 ʱ����ACP ����BPQ �Ƿ�ȫ�ȣ� ���жϴ�ʱ�߶� PC ���߶� PQ ��λ�ù�ϵ����ֱ�˵�����ɣ�
��2����ͼ��2��������AC��AB��BD��AB�� ��Ϊ ����CAB=��DBA=60�㡱���� Q ���˶��� ��Ϊ x cm/s�������������䣬���� P��Q �˶���ij��ʱ������ACP ����BPQ ȫ�ȣ������Ӧ�� x��t ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������������������������λ��ijУ�ڿ�չ�������������ļ�ֵ����Ϊ��������Ļ�У���һ����ƻ���2������������2����������Ϊ��������������ѡȡ2�ݽ��н�����������״ͼ�������㣬����ѡȡ��2�������У���������Ϊ���������ͬʱ�����еĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com