
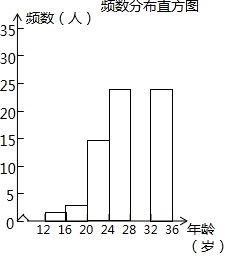
 �ӹ������������������ȹ������е�������ɡ�ȹ�����Ʒ����ʽ�����Ĺ�������ģʽ�ڸ�������Ѹ�ٵ��ռ������ݹ�����Ϣ���ķ������й��������÷�չ����2017��ʾ�����빲�����û��6 ���ˣ�����һ������Լ1���ˣ�
�ӹ������������������ȹ������е�������ɡ�ȹ�����Ʒ����ʽ�����Ĺ�������ģʽ�ڸ�������Ѹ�ٵ��ռ������ݹ�����Ϣ���ķ������й��������÷�չ����2017��ʾ�����빲�����û��6 ���ˣ�����һ������Լ1���ˣ�| ����Σ��꣩ | Ƶ�� | Ƶ�� |
| 12��x��16 | 2 | 0.02 |
| 16��x��20 | 3 | 0.03 |
| 20��x��24 | 15 | a |
| 24��x��28 | 25 | 0.25 |
| 28��x��32 | b | 0.30 |
| 32��x��36 | 25 | 0.25 |
���� ��1�����ݳ�������Ķ���ɵã�
��2���ٸ��ݡ�Ƶ��=Ƶ�����������ɷֱ����a��b��ֵ��
���ɢ����������ݿɲ�ȫͼ�Σ�
�����������������е�3��4��5���Ƶ��֮�Ϳɵô𰸣�
��� �⣺��1�����鷽ʽ�бȽϺ�������C��
�ʴ�Ϊ��C��
��2����a=15��100=0.15��b=100��0.3=30��
�ʴ�Ϊ��0.15��30��
�ڲ�ȫͼ�����£�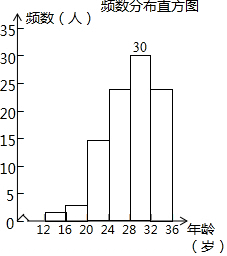
��1000����0.15+0.25+0.3��=700���ˣ���
�𣺹����������������20�굽32�꣨��20�꣬����32�꣩�ﹲ������������700�ˣ�
���� ���⿼������ͼ��Ƶ�ʷֲ������������������֪ʶ������Ĺؼ��Ǽ�סƵ��=Ƶ����������Ƶ��֮��Ϊ1�������п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
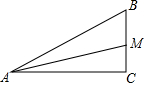 ��ͼ���ڡ�ABC�У���C=90�㣬AM�ǡ�BAC��ƽ���ߣ�CM=20cm����ôM��AB�ľ���Ϊ20cm��
��ͼ���ڡ�ABC�У���C=90�㣬AM�ǡ�BAC��ƽ���ߣ�CM=20cm����ôM��AB�ľ���Ϊ20cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
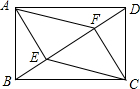 ��ͼ���ھ���ABCD�У�BDΪ�Խ��ߣ���E��F���߶�BD�ϵĵ㣬��BE=DF������AE��EC��CF��FA��
��ͼ���ھ���ABCD�У�BDΪ�Խ��ߣ���E��F���߶�BD�ϵĵ㣬��BE=DF������AE��EC��CF��FA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2 | B�� | y1��y2 | C�� | y1=y2 | D�� | y1��y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
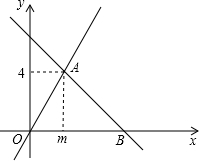 ��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=-x+n��ͼ��������������y=2x��ͼ���ڵ�A��m��4����
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=-x+n��ͼ��������������y=2x��ͼ���ڵ�A��m��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
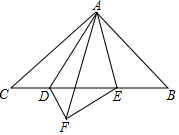 ��֪����ͼ����ABC�У���CAB=90�㣬AC=AB����D��E��BC�ϵ����㣬�ҡ�DAE=45�㣬��ADC���ADF����ֱ��AD�Գƣ���֤����1����FAE=��BAE��
��֪����ͼ����ABC�У���CAB=90�㣬AC=AB����D��E��BC�ϵ����㣬�ҡ�DAE=45�㣬��ADC���ADF����ֱ��AD�Գƣ���֤����1����FAE=��BAE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com