
 已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A,B.
已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A,B.分析 (1)把A(2,a)代入y1=$\frac{4}{x}$即可求得a,然后代入直线y3=-x+b即可求得b;
(2)根据直线的解析式求得直线与x轴的交点坐标,然后根据S△OAB=S△AOC+S△BOC即可求得;
(3)根据图象即可求得.
解答 解:(1)∵点A是反比例函数y1=$\frac{4}{x}$图象上的点,
∴a=$\frac{4}{2}$=2,
∴A(2,2),
∵点A在直线y3=-x+b上,
∴2=-2+b,
∴b=4.
(2)设直线与x轴的交点为C,
由直线y3=-x+4可知直线与x轴的交点坐标为C(4,0),
解$\left\{\begin{array}{l}{y=-x+4}\\{y=-\frac{5}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=5}\end{array}\right.$,$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$,
∴B(5,-1),
∴=$\frac{1}{2}$×4×2+$\frac{1}{2}$×4×1=6;
(3)由图象可知:y2>y3时x的取值范围为x>5.
点评 本题考查了反比例函数和一次函数的交点问题,待定系数法求一次函数的解析式以及函数图象上点的坐标特征;数形结合思想的运用是本题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4<$\sqrt{11}$<5 | B. | (x+1)(x+2)=x2+3x+2 | C. | 2-3=3-2 | D. | x3•x2=x3-x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
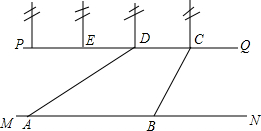 如图,河流的两岸MN,PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C,D,E…某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了120m到达B处,测得∠CBN=60°.求河流的宽度.(结果精确到0.1m)
如图,河流的两岸MN,PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C,D,E…某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了120m到达B处,测得∠CBN=60°.求河流的宽度.(结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com