
 如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.分析 (1)只要证明∠A+∠B=90°,∠ADE+∠B=90°即可解决问题;
(2)首先证明AC=2DE=20,在Rt△ADC中,DC=$\sqrt{2{0}^{2}-1{6}^{2}}$=12,设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2-202,可得x2+122=(x+16)2-202,解方程即可解决问题;
解答 (1)证明:连接OD,
∵DE是切线,
∴∠ODE=90°,
∴∠ADE+∠BDO=90°,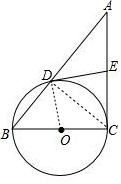
∵∠ACB=90°,
∴∠A+∠B=90°,
∵OD=OB,
∴∠B=∠BDO,
∴∠ADE=∠A.
(2)连接CD.
∵∠ADE=∠A,
∴AE=DE,
∵BC是⊙O的直径,∠ACB=90°,
∴EC是⊙O的切线,
∴ED=EC,
∴AE=EC,
∵DE=10,
∴AC=2DE=20,
在Rt△ADC中,DC=$\sqrt{2{0}^{2}-1{6}^{2}}$=12,
设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2-202,
∴x2+122=(x+16)2-202,
解得x=9,
∴BC=$\sqrt{1{2}^{2}+{9}^{2}}$=15.
点评 本题考查切线的性质、勾股定理、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
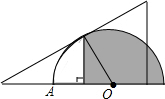 如图,将一块含30°角的直角三角版和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=4,则图中阴影部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$.(结果保留π)
如图,将一块含30°角的直角三角版和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=4,则图中阴影部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
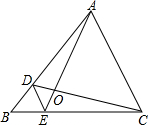 如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若AD=3BD,则S△DOE:S△AOC的值为( )
如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若AD=3BD,则S△DOE:S△AOC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | |$\frac{1}{2}$-2|=-$\frac{3}{2}$ | C. | $\root{3}{8}$=2$\sqrt{2}$ | D. | ($\frac{1}{2}$)-1=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )
如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )| A. | $\frac{4π}{3}$$-\sqrt{3}$ | B. | $\frac{4π}{3}$-2$\sqrt{3}$ | C. | $\frac{2π}{3}$$-\sqrt{3}$ | D. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
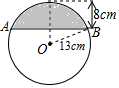 如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )| A. | 10cm | B. | 16cm | C. | 24cm | D. | 26cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )| A. | 10m | B. | 12m | C. | 12.4m | D. | 12.32m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,2) | B. | (-4,2) | C. | (-1,5) | D. | (-1,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com