
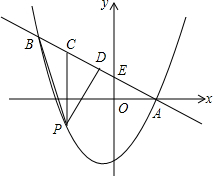
 ��ͼ��ֱ��y=-$\frac{1}{2}$x+1��y�ύ�ڵ�E����������y=ax2-bx-3����A��B���㣬��A��x���ϣ���B��������Ϊ3����P��ֱ��A��B�·�����������һ���㣨����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D��
��ͼ��ֱ��y=-$\frac{1}{2}$x+1��y�ύ�ڵ�E����������y=ax2-bx-3����A��B���㣬��A��x���ϣ���B��������Ϊ3����P��ֱ��A��B�·�����������һ���㣨����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D������ ��1�������A��B������꣬������������߽���ʽ���ɣ�����cos��CPD��ֵʱ�����ýǵĹ�ϵ���ó���CPD���ABF���࣬�����ABF������ֵ��������
��2��������֪�ɵ�PB=PA���������ľ��룬�����������ʱm��ֵ���ڴ��������꣬�ҳ��߶εij��ȵı���ʽ���䷽���ɵó����ۣ��ۼ�����ڣ����õȵ������ε�����ȵ�����ߵıȣ��������mֵ��
��� �⣺��1������B��BF��x���ڵ�F����ͼ1��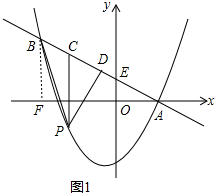
�ߵ�A��x���ϣ���B��������Ϊ3����A��B�������ֱ��y=-$\frac{1}{2}$x+1�ϣ�
�ཫy=0��y=3����ֱ�߷��̽��x=2��x=-4��
���A��2��0������B��-4��3����
��AF=2-��-4��=6��BF=3-0=3��AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=3$\sqrt{5}$��
��A��B�������������ϣ�
��$\left\{\begin{array}{l}{0=4a-2b-3}\\{3=16a+4b-3}\end{array}\right.$�����$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$��
�������߽���ʽΪy=$\frac{1}{2}$x2+$\frac{1}{2}$x-3��
��PC��x�ᣬPD��AB��BF��x�ᣬ
���ABF=��PCD����ABF+��BAF=90�㣬��PCD+��CPD=90�㣬
��cos��CPD=sin��ABF=$\frac{AF}{AB}$=$\frac{6}{3\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$��
��2��������AP����ͼ2��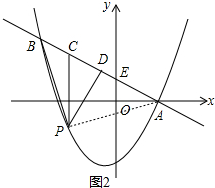
��PD��AB�ڵ�D����AD=BD��
��PA=PB��
��P��������m��$\frac{1}{2}$m2+$\frac{1}{2}$m-3������A��2��0������B��-4��3����
���������빫ʽ��֪��
PA2=��m-2��2+${��\frac{1}{2}{m}^{2}+\frac{1}{2}m-3��}^{2}$��PB2=��m+4��2+${��\frac{1}{2}{m}^{2}+\frac{1}{2}m-6��}^{2}$��
����m2-3m-39=0��
���m=$\frac{3-\sqrt{61}}{2}$��m=$\frac{3+\sqrt{61}}{2}$��1����ȥ����
���P��������$\frac{3-\sqrt{61}}{2}$��$\frac{19-2\sqrt{61}}{2}$����
�ʴ��ڵ�P��ʹAD=BD��P������Ϊ��$\frac{3-\sqrt{61}}{2}$��$\frac{19-2\sqrt{61}}{2}$����
�ڡ�P������Ϊ��m��$\frac{1}{2}$m2+$\frac{1}{2}$m-3����C������Ϊ��m��1-$\frac{1}{2}$m����
PC=1-$\frac{1}{2}$m-��$\frac{1}{2}$m2+$\frac{1}{2}$m-3��=-$\frac{1}{2}$m2-m+4��
PD=PC•cos��CPD=-$\frac{\sqrt{5}}{5}$m2-$\frac{2\sqrt{5}}{5}$m+$\frac{8\sqrt{5}}{5}$=-$\frac{\sqrt{5}}{5}$��m+1��2+$\frac{9\sqrt{5}}{5}$��
��m=-1ʱ��PD���ʱPD=$\frac{9\sqrt{5}}{5}$��
�ۼ�����������ĵ�P���ӳ�PC������B��BM��PC��M�㣬����D��DN��PC��N�㣬��ͼ3��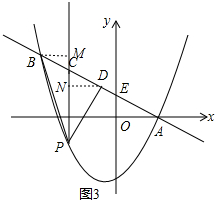
��P������Ϊ��m��$\frac{1}{2}$m2+$\frac{1}{2}$m-3����C������Ϊ��m��1-$\frac{1}{2}$m����B�����꣨-4��3����
��BM=4+m��
���߶�PC�ѡ�PDB�ֳ����������Σ�ʹ�����������ε������Ϊ3��4��
a��$\frac{ND}{BM}$=$\frac{4}{3}$��
��ND=$\frac{4}{3}$BM��CD=$\frac{ND}{cos��CPD}$��PC=$\frac{CD}{sin��CPD}$��
��cos��CPD=$\frac{2\sqrt{5}}{5}$��sin2��CPD+cos2��CPD=1��
��sin��CPD=$\frac{\sqrt{5}}{5}$��
��PC=$\frac{10}{3}$BM=$\frac{10}{3}$��4+m��=-$\frac{1}{2}$m2-m+4����3m2+26m+56=0��
���m=-$\frac{14}{3}$��-4����ȥ������m=-4����ȥ����
b��$\frac{ND}{BM}$=$\frac{3}{4}$��
��ND=$\frac{3}{4}$BM��CD=$\frac{ND}{cos��CPD}$��PC=$\frac{CD}{sin��CPD}$��
��cos��CPD=$\frac{2\sqrt{5}}{5}$��sin2��CPD+cos2��CPD=1��
��sin��CPD=$\frac{\sqrt{5}}{5}$��
��PC=$\frac{15}{8}$BM=$\frac{15}{8}$��4+m��=-$\frac{1}{2}$m2-m+4����4m2+23m+28=0��
���m=-$\frac{7}{4}$����m=-4����ȥ����
�ۺ�a��b��֪�������ʺϵ�m��ֵ��ʹ�����������ε������Ϊ3��4��m��ֵΪ-$\frac{7}{4}$��
���� ���⿼���˶��κ�����Ӧ�á����������ε����ʡ������ľ��빫ʽ�Լ������䷽����ֵ�ȣ�����Ĺؼ��ǻ���ͼ�Σ��������ν��Ѱ�ұ߽ǵĵ�����ϵ��


 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3m2n��3nm2 | B�� | $-\frac{1}{4}{x^2}{y^{c+6}}$xy2��2x2+ay3x2y2 | ||
| C�� | -5ab��-5��103ab | D�� | 35��-12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���������� | B�� | ƽ���������� | C�� | ������ƽ���� | D�� | ��ƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��7x=4x-3�����7x-4x=3 | |
| B�� | ��$\frac{2x-1}{3}=1+\frac{x-3}{2}$ȥ��ĸ��2��2x-1��=1+3��x-3�� | |
| C�� | ��2��2x-1��-3��x-3��=1ȥ���ŵ�4x-2-3x-9=1 | |
| D�� | ��2x+1=x+7����ϲ�ͬ�����x=6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5a2-4a2=1 | B�� | 3a+2b=5ab | C�� | 2ab2+3a2b=5a3b3 | D�� | 2x2y-3x2y=-x2y |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com