
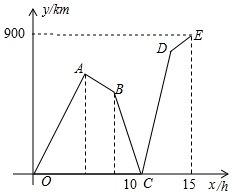
 一列快车和一列慢车同时从甲地出发,分别以速度v1、v2(单位:km/h,且v1>2v2)匀速驶向乙地.快车到达乙地后停留了2h,沿原路仍以速度v1匀速返回甲地.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示从慢车出发至慢车到达乙地的过程中,y与x之间的函数关系.根据图象进行以下探究:
一列快车和一列慢车同时从甲地出发,分别以速度v1、v2(单位:km/h,且v1>2v2)匀速驶向乙地.快车到达乙地后停留了2h,沿原路仍以速度v1匀速返回甲地.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示从慢车出发至慢车到达乙地的过程中,y与x之间的函数关系.根据图象进行以下探究:分析 (1)由图象即可得到结论;
(2)根据图象,得到慢车的速度为$\frac{900}{15}$=60(km/h),快车的速度为$\frac{900×2-10×60}{8}$=150(km/h),于是得到结论;
(3)根据每段的函数解析式即可得到结论.
解答 解:(1)由图象知,甲、乙两地之间的距离为900km,
故答案为:900;
(2)根据图象,得慢车的速度为$\frac{900}{15}$=60(km/h),
快车的速度为$\frac{900×2-10×60}{8}$=150(km/h),
所以线段AB所表示的y与x之间的函数表达式为y1=900-60x,
所以线段CD所表示的y与x之间的函数表达式为
y2=(60+150)(x-10)=210x-2100;
(3)①线段OA所表示的y与x之间的函数表达式为y3=90x(0≤x<6),
令y3=480,得x=$\frac{16}{3}$,
②线段AB所表示的y与x之间的函数表达式为y1=-60x+900(6≤x<8),
令y1=480,得x=7,
③线段CD所表示的y与x之间的函数表达式为y2=210x-2100(10≤x<14),
令y2=480,得x=$\frac{86}{7}$.
答:慢车出发$\frac{16}{3}$h、7h、$\frac{86}{7}$h后,两车相距480km.
点评 此题主要考查了一次函数的应用,利用图表中数据得出慢车速度是解题关键.


科目:初中数学 来源: 题型:解答题
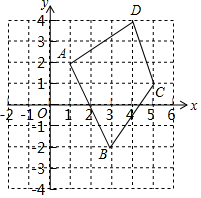 如图所示的直角坐标系中,四边形ABCD的四个顶点的坐标分别是:A(1,2),B(3,-2),C(5,1),D(4,4)
如图所示的直角坐标系中,四边形ABCD的四个顶点的坐标分别是:A(1,2),B(3,-2),C(5,1),D(4,4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
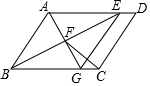 已知:如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过点A作BE的垂线交BE于点F,交BC于点G,连接EG,CF.
已知:如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过点A作BE的垂线交BE于点F,交BC于点G,连接EG,CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8.
如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
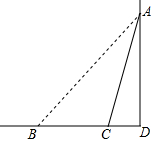 如图所示,一块广告牌AB顶端固定在一堵墙AD的A点处,与地面夹角∠ABD=45°,由于施工底部断裂掉一段以后,底部落在距离B点8米处的C点,此时与地面夹角∠ACD=75°.求断裂前、后的广告牌AB、AC的长度.
如图所示,一块广告牌AB顶端固定在一堵墙AD的A点处,与地面夹角∠ABD=45°,由于施工底部断裂掉一段以后,底部落在距离B点8米处的C点,此时与地面夹角∠ACD=75°.求断裂前、后的广告牌AB、AC的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com