
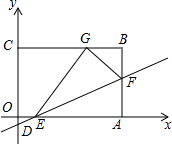
 ��ͼ������OABC�ı�OA��x���ϣ���OC��y���ϣ���B�ڵ�һ���ޣ�ֱ��y=$\frac{1}{3}$x-1��x�ᡢy�ᡢ��AB�ֱ��ڵ�E����D����F������AEF��ֱ��EF�۵�����Aǡ������BC�ߵĵ�Gλ���ϣ��߶�AF��BF�ij���һԪ���η���x2-9x+20=0��������AF��BF����
��ͼ������OABC�ı�OA��x���ϣ���OC��y���ϣ���B�ڵ�һ���ޣ�ֱ��y=$\frac{1}{3}$x-1��x�ᡢy�ᡢ��AB�ֱ��ڵ�E����D����F������AEF��ֱ��EF�۵�����Aǡ������BC�ߵĵ�Gλ���ϣ��߶�AF��BF�ij���һԪ���η���x2-9x+20=0��������AF��BF�������� ��1����ֱ��y=$\frac{1}{3}$x-1����y=0���ⷽ�̼������E�����꣬�����߶�AF��BF�ij���һԪ���η���x2-9x+20=0��������AF��BF���������AF�ij����Ӷ����F�����ꣻ
��2�����ݹ��ɶ������BG�ij������G�����꣬Ȼ����ݴ���ϵ�����������ֱ��EG�Ľ���ʽ��
��3������ƽ���ı��ε����ʵó�M��N����������ȣ���M��N��������Ϊn����n=$\frac{1}{3}$x-1��n=$\frac{3}{4}$x-$\frac{9}{4}$�����M��N�ĺ����꣬Ȼ�����|xM-xN|=OE=3���������n��ֵ�������Ϳ����M��N�����꣮
��� �⣨1����ֱ��y=$\frac{1}{3}$x-1��x�ύ�ڵ�E��
����y=0����$\frac{1}{3}$x-1=0�����x=3��
��E��3��0����
���߶�AF��BF�ij���һԪ���η���x2-9x+20=0��������AF��BF����
��AF=5��BF=4��
��F���������Ϊ5��
��y=5����y=$\frac{1}{3}$x-1�ã�5=$\frac{1}{3}$x-1�����x=18��
��F��18��5����
��2����GF=AF=5��BF=4��
��BG=$\sqrt{G{F}^{2}-B{F}^{2}}$=3��
��CG=8-3=15��
��AB=AF+BF=9��
��G��15��9����
��ֱ��EG�Ľ���ʽΪy=kx+b��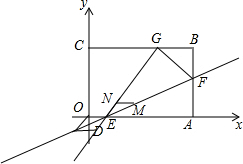
��$\left\{\begin{array}{l}{15k+b=9}\\{3k+b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-\frac{9}{4}}\end{array}\right.$��
����EG�Ľ���ʽΪy=$\frac{3}{4}$x-$\frac{9}{4}$��
��3�����ڣ�
���ɣ����Ե�O����E����M����NΪ������ı���Ϊƽ���ı��Σ���ͼ��
��M��N����������ȣ���M��N��������Ϊn����n=$\frac{1}{3}$x-1��n=$\frac{3}{4}$x-$\frac{9}{4}$��
���xM=3n+3��xN=$\frac{4n+9}{3}$��
��������|xM-xN|=OE=3��
��xM-xN=��3��
��xM-xN=3ʱ��3n+3-$\frac{4n+9}{3}$=3�����n=$\frac{9}{5}$��
��xM-xN=-3ʱ��3n+3-$\frac{4n+9}{3}$=-3�����n=-$\frac{9}{5}$��
��n=$\frac{9}{5}$����xM=3n+3��xN=$\frac{4n+9}{3}$���ã�xM=$\frac{42}{5}$��xN=$\frac{27}{5}$��
��n=-$\frac{9}{5}$����xM=3n+3��xN=$\frac{4n+9}{3}$���ã�xM=-$\frac{12}{5}$��xN=$\frac{3}{5}$��
���M��������$\frac{42}{5}$��$\frac{9}{5}$����-$\frac{12}{5}$��-$\frac{9}{5}$������N��������$\frac{27}{5}$��$\frac{9}{5}$����$\frac{3}{5}$��-$\frac{9}{5}$����
���� ������һ�κ������ۺ��⣬�����˽�һԪ���η��̣����ɶ�����Ӧ�ã�����ϵ������һ�κ����Ľ���ʽƽ���ı��ε����ʵȣ���ȷ���F�������ǽ������Ĺؼ���


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 49 | B�� | 7 | C�� | 13 | D�� | $\sqrt{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
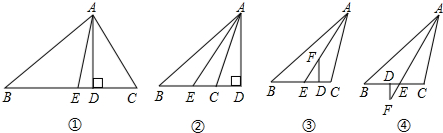
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| 1 | 1 | 1 | 1 | 1 | �� |
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 3 | 5 | 7 | 9 | |
| 1 | 4 | 7 | 10 | 13 | |
| 1 | 5 | 9 | 13 | 17 | |
| �� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���е������������������ϵĵ��ʾ | |
| B�� | ���Ų�ͬ����������Ϊ�෴�� | |
| C�� | ������ӣ���һ�������κ�һ���� | |
| D�� | �����������һ��С�ڱ����� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com