
分析 (1)先通分,再把分子相加减,分式化为最简分式后把a=3代入进行计算即可;
(2)先算括号里面的,再算乘法,最后把x的值代入进行计算即可.
解答 解:(1)原式=$\frac{(a+1)^{2}}{(a+1)(a-1)}$-$\frac{a}{a-1}$
=$\frac{a+1}{a-1}$-$\frac{a}{a-1}$
=$\frac{1}{a-1}$,
当a=3时,原式=$\frac{1}{2}$;
(2)原式=$\frac{3x(x+1)-x(x-1)}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{3{x}^{2}+3x-{x}^{2}+x}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{2{x}^{2}+4x}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{2x(x+2)}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=2x+4,
当x=$\frac{1}{2}$时,原式=1+4=5.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


科目:初中数学 来源: 题型:选择题
| A. | 16$\sqrt{3}$cm | B. | 8$\sqrt{3}$cm | C. | 4$\sqrt{3}$cm | D. | 16cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
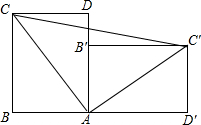 一个直立的火柴盒在桌面上倒下,启发人们发现了勾股定理的一种新的证法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a.BC=b,AC=c,请利用四边形BCC′C的面积证明勾股定理.
一个直立的火柴盒在桌面上倒下,启发人们发现了勾股定理的一种新的证法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a.BC=b,AC=c,请利用四边形BCC′C的面积证明勾股定理.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ② | B. | ③ | C. | ① | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在梯形ABCD中,上底AD=$\sqrt{12}$,下底BC=$\sqrt{48}$,高AE=$\sqrt{27}$,求梯形ABCD的面积.
已知:如图,在梯形ABCD中,上底AD=$\sqrt{12}$,下底BC=$\sqrt{48}$,高AE=$\sqrt{27}$,求梯形ABCD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平面直角坐标系中,矩形OABC放置如图,点A(3,0)、C(0,9),现将它绕点B逆时针旋转得矩形O′A′BC′,点O的对应点O′在x轴上,O′C′交AB于D.
平面直角坐标系中,矩形OABC放置如图,点A(3,0)、C(0,9),现将它绕点B逆时针旋转得矩形O′A′BC′,点O的对应点O′在x轴上,O′C′交AB于D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com