
分析 首先判断出每个数的正负,然后根据每个数的分子分别是5、7、9、11、…,判断出第n个数的分子是多少;最后根据每个数的分母分别是4、9、16、25、…,判断出第n个数的分母是多少,进而判断出这组数的第n个数是多少,再把n=19代入,求出第19个数数据为多少即可.
解答 解:∵这组数分别是负数、正数、负数、正数、…,
∴这组数的第n个数的正负即(-1)n的正负;
∵5=2×1+3,7=2×2+3,9=2×3+3,11=2×4+3,
∴第n个数的分子是:2n+3;
∵4=(1+1)2,9=(2+1)2,16=(3+1)2,25=(4+1)2,
∴第n个数的分母是:(n+1)2;
∴这组数的第n个数是:
(-1)n•$\frac{2n+3}{{(n+1)}^{2}}$
∴第19个数据是:
(-1)19•$\frac{2×19+3}{{(19+1)}^{2}}$=-$\frac{41}{400}$.
故答案为:-$\frac{41}{400}$.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是求出这组数的第n个数是多少.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 96 | 110 | 90 | 104 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x-11)=180 | B. | 2x+2(x-11)=180 | C. | x(x+11)=180 | D. | 2x+2(x+11)=180 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{7}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
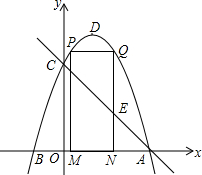 如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.
如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com