
 ���ǽ�ʹ�ú���ֵΪ����Ա�����ֵ��Ϊ���������ֵ����ʱ�ĵ��Ϊ��������㣮���磬���ں���y=x-1����y=0���ɵ�x=1�����Ǿ�˵1�Ǻ���y=x-1�����ֵ���㣨1��0���Ǻ���y=x-1����㣮��֪���κ���y=kx2-��4k+1��x+3k+3��
���ǽ�ʹ�ú���ֵΪ����Ա�����ֵ��Ϊ���������ֵ����ʱ�ĵ��Ϊ��������㣮���磬���ں���y=x-1����y=0���ɵ�x=1�����Ǿ�˵1�Ǻ���y=x-1�����ֵ���㣨1��0���Ǻ���y=x-1����㣮��֪���κ���y=kx2-��4k+1��x+3k+3������ ��1����y=0���ɽ��x��ֵ���ɺ�����������㶼�������㣬�ɵ�$\frac{1}{k}$�����������ɵó�k��ֵ��
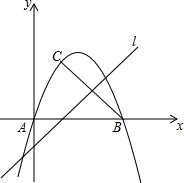
��2����k��0���ɵ�������һ�κ����Ĺ�ϵʽ���ɶ��κ������������ֱ��ǵ�A��B����A�ڵ�B����ࣩ���ɵ�A��B���꣬��y=-kx����ƽ��n����λ���ɵ�l�Ľ���ʽΪy=x-n���ɵ�B����ֱ��l�ĶԳƵ�C�����ڵ�B����l��BC����ֱ��BC�Ľ���ʽΪy=-x+m���ѵ�B��3��0������ɵ�m��ֵ���ɵó�ֱ��BC�Ľ���ʽΪy=-x+3��ֱ��BC�Ľ���ʽ�������������г����̽��x��y���ɵó�C�����꣬�ɵó��߶�BC���е����꣬�ѣ�2��1������y=x-n����1=2-n�����n=1�����ɵó�l�Ľ���ʽ��
��3��ȷ����ֱ��ƽ����l������������һ������ʱ����MEF��������ֵ����G���ڵ�ֱ��Ϊy=x+b���ɡ�=0�����b��ֵ���ɵ�G���ڵ�ֱ��Ϊy=x+1�����á�MNQ�ǵ���ֱ�������Σ��ɵó�ƽ����ľ��룬����S��MEF=$\frac{1}{2}$EF•MN��⼴�ɣ�
��� �⣺��1����y=0����kx2-��4k+1��x+3k+3=0�����x=$\frac{4k+1��\sqrt{��4k+1��^{2}-4k��3k+3��}}{2k}$��
��x=3��x=1+$\frac{1}{k}$��
�ߺ�����������㶼�������㣬
��$\frac{1}{k}$��������
��k=��1��
��2���ߵ�k��0��
��k=-1��
��y=-x2+3x��y=4x+3��
�߶��κ������������ֱ��ǵ�A��B����A�ڵ�B����ࣩ��
��A��0��0����B��3��0����
��y=-kx����ƽ��n����λ��
��l�Ľ���ʽΪy=x-n��
�ߵ�B����ֱ��l�ĶԳƵ�C�����ڵ�B����
��l��BC��
����ֱ��BC�Ľ���ʽΪy=-x+m��
�ѵ�B��3��0�������0=-3+m�����m=3��
��ֱ��BC�Ľ���ʽΪy=-x+3��
ֱ��BC�Ľ���ʽ��������������$\left\{\begin{array}{l}{y=-x^2+3x}\\{y=-x+3}\end{array}\right.$�����$\left\{\begin{array}{l}{{x}_{1}=3}\\{{y}_{1}=0}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=2}\end{array}\right.$��
��C��1��2����
�߶�BC���е�����Ϊ��$\frac{1+3}{2}$��$\frac{0+2}{2}$��������2��1����
�ѣ�2��1������y=x-n����1=2-n�����n=1��
��l�Ľ���ʽΪy=x-1��
��3����ͼ������G��ֱ��MG��y���ڵ�M����MN��l��l�ڵ�N��
��ֱ��ƽ����l������������һ������ʱ����MEF��������ֵ��
��G���ڵ�ֱ��Ϊy=x+b����y=-x2+3x������x+b=-x2+3x�������x2-2x+b=0��
��=4-4b=0�����b=1��
��G���ڵ�ֱ��Ϊy=x+1��
��MQ=1-��-1��=2��
�ߡ�MNQ�ǵ���ֱ�������Σ�
��MN=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$��
��S��MEF=$\frac{1}{2}$EF•MN=$\frac{1}{2}$��3��$\sqrt{2}$=$\frac{3\sqrt{2}}{2}$��
���� ������Ҫ�����˶��κ����뷽�̡�����֪ʶ���ۺ�Ӧ�ã��漰һ�κ��������κ����Ľ���ʽ��һԪ���η��̵�֪ʶ������Ĺؼ���ע�����ν�ϵ���ѧ˼������ã����ڸ��Ѷȵ��⣮


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
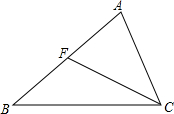 ��ͼ��F�ǡ�ABC��AB����һ�㣬���н�����ȷ�ĸ����ǣ�������
��ͼ��F�ǡ�ABC��AB����һ�㣬���н�����ȷ�ĸ����ǣ�������| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
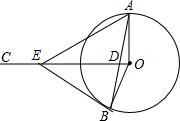 ��ͼ��OA��OB�ǡ�O�İ뾶������O��OC��OA������AB�ڵ�D����E��BD�Ĵ�ֱƽ������OC�Ľ��㣬����BE
��ͼ��OA��OB�ǡ�O�İ뾶������O��OC��OA������AB�ڵ�D����E��BD�Ĵ�ֱƽ������OC�Ľ��㣬����BE�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
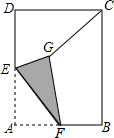 ��ͼ���ھ���ABCD�У�AD=6��CD=4��AD���е�ΪE����F��AB����һ�㣨����A��B�غϣ�������EF���ѡ�A��EF�۵���ʹ��A���ڵ�G��������CG�����߶�CG��ȡֵ��Χ��$\frac{2}{5}$$\sqrt{37}$��CG��2$\sqrt{13}$��
��ͼ���ھ���ABCD�У�AD=6��CD=4��AD���е�ΪE����F��AB����һ�㣨����A��B�غϣ�������EF���ѡ�A��EF�۵���ʹ��A���ڵ�G��������CG�����߶�CG��ȡֵ��Χ��$\frac{2}{5}$$\sqrt{37}$��CG��2$\sqrt{13}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
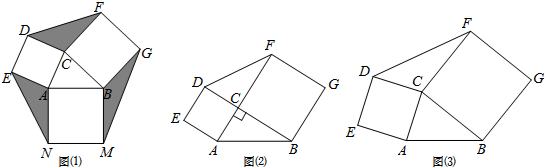
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com