
【题目】我们把使得函数值为零的自变量的值称为函数的零点. 例如,对于函数y=-x+1,令y=0,可得x=1,我们就说x=1是函数y=-x+1的零点.己知函数y=x2-2(m+1)x-2(m+2)
(m为常数) .(1)当m=-1时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为![]() 和
和![]() ,且
,且![]() ,求此时的函数解析式,并判断点(n+2,n2-10)是否在此函数的图象上.
,求此时的函数解析式,并判断点(n+2,n2-10)是否在此函数的图象上.
【答案】(1)、x=±![]() ;(2)、证明过程见解析;(3)、在,理由见解析.
;(2)、证明过程见解析;(3)、在,理由见解析.
【解析】
试题分析:(1)、首先求出m=-1时的函数解析式,然后令y=0求出x的值;(2)、根据y=0求出方程的根的判别式,然后得出判别式为非负数得出答案;(3)、根据韦达定理和已知条件求出m的值,然后得出二次函数的解析式,最后将x=n+2代入函数解析式看y值与已知的是否相等.
试题解析:(1)、当![]() 时,该函数为
时,该函数为![]() ,令
,令![]() ,可得
,可得![]() .
.
∴当![]() 时,该函数的零点为
时,该函数的零点为![]() 和
和![]() .
.
(2)、令![]() ,得
,得![]()
∴无论![]() 取何值时,方程
取何值时,方程![]() 总有两个不相等的实数根,即无论
总有两个不相等的实数根,即无论![]() 取何值,该函数总有两个两个零点.
取何值,该函数总有两个两个零点.
(3)、根据题意,得,![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,解得
,解得![]() .
.
∴函数的解析式为![]() .∴配方得,
.∴配方得,![]() ,把
,把![]() 代入可得
代入可得![]() .
.
∴点![]() 在函数
在函数![]() 的图象上.
的图象上.


科目:初中数学 来源: 题型:
【题目】截止2019年12月,全国农村公路总里程已超过404万公里,为打赢脱贫攻坚战提供了有力保障.将“404万”用科学记数法可表示为( )
A.404×104B.4.04×105C.4.04×106D.4.04×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为确保信息安全,信息需加密传输,发送方由明文→密文(加密);接收方由密文→明文(解密).已知加密规则为:明文a,b,c,d对应的密文为a+b,b+c,c+d,d+2a.例如:明文1,2,3,4对应的密文为3,5,7,6.当接收方收到密文8,11,15,15时,则解密得到的明文应为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB =AC=2,∠B = 40°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE = 40°,DE交线段AC于点E.
(1)当∠BDA = 115°时,∠BAD= °,∠DEC = °,当点D从点B向点C运动时,∠BDA逐渐变 (填“大”或“小”) .
(2)当DC等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列推理过程,在括号中填写理由. 已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2()
∵AC∥DE(已知)
∴∠1=∠3()
故∠2=∠3()
∵DF∥AE(已知)
∴∠2=∠5()
∴∠3=∠4()
∴DE平分∠BDE()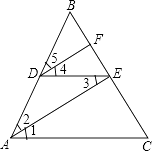
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com