
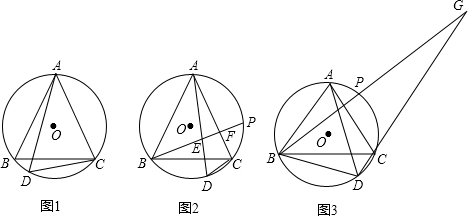
分析 (1)由∠B=∠D,∠ADC=∠ACB,即可得∠B=∠ACB,则可证得AB=AC;
(2)首先连接AP,可得∠PBC=∠ABC-∠ABP=∠APB-∠ABP,由AE=AF,易得∠PBC=∠BAD-∠PAC,继而可证得:∠BCD=2∠PBC;
(3)首先连接PC,PD,作PH⊥DG于点H,过点B作BM⊥DG于点M,易求得PD=PG,即可得∠PCH=∠PBD=45°,然后设PH=CH=x,易得方程在Rt△PHG中,x2+(3-x)2=($\sqrt{5}$)2,继而求得x的值,再设BM=m,即可得m2+(2m-3)2=32,继而求得答案.
解答 (1)证明:∵$\widehat{AC}$=$\widehat{AC}$,
∴∠ADC=∠ABC,
∵∠ADC=∠ACB,
∴∠ABC=ACB,
∴AB=AC; (2)如图2,连接AP,
(2)如图2,连接AP,
∵∠ABC=∠ACB=∠APC,
∴∠PBC=∠ABC-∠ABP=∠APB-∠ABP,
∵AE=AF,
∴∠AEF=∠AFE,
∵∠APB=∠AFE-∠PAC,∠ABP=∠AEF-∠BAD,
∴∠PBC=(∠AFE-∠PAC)-(∠AEF-∠BAD)=∠BAD-∠PAC,
∵∠PAC=∠PBC,
∴∠PBC=∠BAD-∠PBC,
∴∠BAD=2∠PBC,
∴∠BCD=∠BAD=2∠PBC;
(3)如图3,连接PC,PD,作PH⊥DG于点H,过点B作BM⊥DG于点M,
∵∠BCD=∠PBC+∠G=2∠PBC,
∴∠PBC=∠G,
∴CG=BC=3,
∵∠PDC=∠PBC=∠G,
∴PD=PG,
∵∠PCH=∠PDC+∠DPC=∠CBP+∠DBC=∠PBD=45°,
∴PH=CH,
设PH=CH=x,
∴HG=3-x,
在Rt△PHG中,x2+(3-x)2=($\sqrt{5}$)2,
解得x=2或x=1
∵∠G=∠PBC<∠PBD,
∴tan∠G<tan45°,
∴x=1,
∴CD=DH-CH=1
设BM=m,
∴MG=2m,
∴CM=2m-3,
∵BC=3,
∴m2+(2m-3)2=32,
解得m=0(舍)或m=$\frac{12}{5}$,
∴DM=$\frac{4}{5}$,
∴BD=$\frac{4\sqrt{10}}{5}$.
点评 此题属于圆的综合题.考查了圆周角定理、等腰三角形的判定与性质、勾股定理以及锐角三角函数的知识.注意准确作出辅助线、掌握方程思想的应用是解此题的关键.


科目:初中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 |
| 2x2-x-2 | -1 | 4 | 13 | 26 |
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解九年级体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩,并按分数段(A:20.5~22.5; B:22.5~24.5; C:24.5~26.5; D:26.5~28.5; E:28.5~30.5)制成如下统计表和条形统计图,请回答下列问题:
为了解九年级体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩,并按分数段(A:20.5~22.5; B:22.5~24.5; C:24.5~26.5; D:26.5~28.5; E:28.5~30.5)制成如下统计表和条形统计图,请回答下列问题:| 分数段 | 频数/人 | 频率 |
| A | 12 | 0.05 |
| B | 11 | a |
| C | 84 | 0.35 |
| D | b | 0.25 |
| E | 48 | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明“六、一”去公园玩投掷飞镖的游戏,投中国中阴影部分由奖品(飞镖盘被平均分成8份),小明一次投镖能获得奖品的概率是( )
小明“六、一”去公园玩投掷飞镖的游戏,投中国中阴影部分由奖品(飞镖盘被平均分成8份),小明一次投镖能获得奖品的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{8}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 入住率 | 0.98 | 0.86 | 0.56 | 0.42 | 0.34 |
| 小区数 | 2 | 4 | 4 | 8 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P60的坐标是(20,0).
如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P60的坐标是(20,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com