
 如图,在△ABC中,点P是BC边上任意一点(点P与点B,C不重合),平行四边形AFPE的顶点F,E分别在AB,AC上.已知BC=2,S△ABC=1.设BP=x,平行四边形AFPE的面积为y.
如图,在△ABC中,点P是BC边上任意一点(点P与点B,C不重合),平行四边形AFPE的顶点F,E分别在AB,AC上.已知BC=2,S△ABC=1.设BP=x,平行四边形AFPE的面积为y.分析 (1)由平行四边形的性质得出PF∥CA,证出△BFP∽△BAC,得出面积比等于相似比的平方,得出S△BFP=$\frac{{x}^{2}}{4}$,同理:S△PEC=($\frac{2-x}{2}$)2,即可得出y与x的函数关系式;
(2)由-$\frac{1}{2}$<0得出y有最大值,把(1)中函数关系式化成顶点式,即可得出结果.
解答 解:(1)∵四边形AFPE是平行四边形,
∴PF∥CA,
∴△BFP∽△BAC,
∴$\frac{{S}_{△BFP}}{{S}_{△BAC}}$=($\frac{x}{2}$)2,
∵S△ABC=1,
∴S△BFP=$\frac{{x}^{2}}{4}$,
同理:S△PEC=($\frac{2-x}{2}$)2,
∴y=1-$\frac{{x}^{2}}{4}$-$\frac{4-4x+{x}^{2}}{4}$,
∴y=-$\frac{{x}^{2}}{2}$+x;
(2)上述函数有最大值,最大值为$\frac{1}{2}$;理由如下:
∵y=-$\frac{{x}^{2}}{2}$+x=-$\frac{1}{2}$(x-1)2+$\frac{1}{2}$,-$\frac{1}{2}$<0,
∴y有最大值,
∴当x=1时,y有最大值,最大值为$\frac{1}{2}$.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质、二次函数的最值;熟练掌握平行四边形的性质,证明三角形相似得出关系式是解决问题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为(1,3)或(5,1).
如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为(1,3)或(5,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,从A地到B地的公路需经过C地,图中AC=50千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A,B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=50千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A,B两地之间修建一条笔直的公路.查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:单选题
如图,直线l:y = 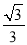 x,过点A(0,1)作y轴的垂线交直线
x,过点A(0,1)作y轴的垂线交直线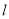 于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )

A. (0,42015) B. (0,42014) C. (0,32015) D. (0,32014)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
| 甲组 | 6.9 | 2.4 | 7 | 91.7% | 16.7% |
| 乙组 | 7 | 1.3 | 7 | 83.3% | 8.3% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com