
【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
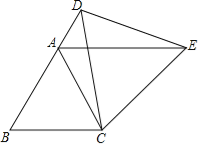
(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
【答案】(1)证明见试题解析;(2)AE∥BC,理由见试题解析.
【解析】试题(1)根据等边三角形各内角为60°和各边长相等的性质可证∠ECA=∠DCB,AC=BC,EC=DC,即可证明△ECA≌△DCB;
(2)根据△ECA≌△DCB可得∠EAC=60°,根据内错角相等,平行线平行即可解题.
证明:(1)∵△ABC、△DCE为等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=∠DBC=60°,
∵∠ACD+∠ACB=∠DCB,∠ECD+∠ACD=∠ECA,
∴∠ECA=∠DCB,
在△ECA和△DCB中,
 ,
,
∴△ECA≌△DCB(SAS);
(2)∵△ECA≌△DCB,
∴∠EAC=∠DBC=60°,
又∵∠ACB=∠DBC=60°,
∴∠EAC=∠ACB=60°,
∴AE∥BC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】东台西瓜食口风味极佳,特别是品牌“王炸”瓜因皮薄肉嫩含水丰富,刀一碰即快速裂开,享誉市场.吴总将一批品牌“王炸”瓜从我市三仓镇运往南京市场进行销售,根据经验,驾驶货车以60千米/小时的平均速度要4小时到达南京市场.
(1)求刘总驾驶货车的汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;
(2)早晨5:00从三仓镇出发,以80千米/小时的平均速度行驶,大概几点到南京市场;
(3)若返回时,刘总全程走高速公路,且匀速行驶,根据规定:最高车速不得超过每小时100公里,最低车速不得低于每小时60公里,试问返程时间的范围是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:
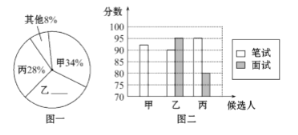
其次,对三名候选人进行了笔试和面试两项测试.各项成绩如右表所示:图二是某同学根据上表绘制的一个不完整的条形图.请你根据以上信息解答下列问题:
(1)补全图一和图二.
(2)请计算每名候选人的得票数.
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面(1)(2)的画图,回答问题(3)(4),如图,P是∠AOB的边OA上一点.
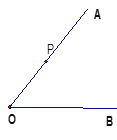
(1)过点P画OB的垂线,垂足为H;
(2)过点P画OA的垂线,交OB于点C;
(3)点O到直线PC的距离是线段_______的长度;
(4)把线段OP、PH和OC按从小到大用“<”连接:_________;理由是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进![]() 、
、![]() 两种文具进行销售.若每个
两种文具进行销售.若每个![]() 种文具的进价比每个
种文具的进价比每个![]() 种文具的进价少2元,且用900元正好可以购进50个
种文具的进价少2元,且用900元正好可以购进50个![]() 种文具和50个
种文具和50个![]() 种文具,
种文具,
(1)求每个![]() 种文具和
种文具和![]() 种文具的进价分别为多少元?
种文具的进价分别为多少元?
(2)若该文具店购进![]() 种文具的数量比购进
种文具的数量比购进![]() 种文具的数量的3倍还少5个,购进两种文具的总数量不超过95个,每个
种文具的数量的3倍还少5个,购进两种文具的总数量不超过95个,每个![]() 种文具的销售价格为12元,每个
种文具的销售价格为12元,每个![]() 种文具的销售价格为15元,则将购进的
种文具的销售价格为15元,则将购进的![]() 、
、![]() 两种文具全部售出后,可使总利润超过371元,通过计算求出该文具店购进
两种文具全部售出后,可使总利润超过371元,通过计算求出该文具店购进![]() 、
、![]() 两种文具有哪几种方案?
两种文具有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.
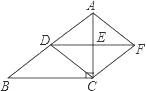
(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com