Question

已知：如下图，四边形ABCD是等腰梯形，其中AD∥BC，AD＝2，BC＝4，AB＝CD＝．点M从点B开始，以每秒2个单位长的速度向点C运动；点N从点D开始，以每秒1个单位长的速度向点A运动，若点M，N同时开始运动，点M与点C不重合，运动时间为t(t＞0)．过点N作NP垂直于BC，交BC于点P，交AC于点Q，连结MQ．

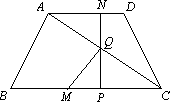
(1)用含t的代数式表示QP的长；

(2)设△CMQ的面积为S，求出S与t的函数关系式；

(3)求出t为何值时，△CMQ为等腰三角形．

(说明：问题(3)是额外加分题，加分幅度为1～4分)

Answer 1

答案：
解析：

(1)过点A作AE⊥BC，交BC于点E，如下图．由AD＝2，BC＝4，AB＝CD＝， 　　得AE＝2．　　(3分) 　　∵ND＝t，∴PC＝1＋t． 　　∴． 　　即．∴．　　(6分) 　　(2)∵点M以每秒2个单位长运动，∴BM＝2t，CM＝4－2t．　　(8分) 　　∴S△CMQ＝＝． 　　即S＝．　　(12分) 　　(3)若QM＝QC，∵QP⊥MC，∴MP＝CP．而MP＝4－(1＋t＋2t)＝3－3t， 　　即1＋t＝3－3t，∴t＝．　　(加1分) 　　若CQ＝CM，∵CQ2＝CP2＋PQ2＝， 　　∴CQ＝．∵CM＝4－2t，∴＝4－2t． 　　∴．　　(加2分) 　　若MQ＝MC，∵MQ2＝MP2＋PQ2＝， 　　∴＝，即． 　　解得t＝或t＝－1(舍去)．∴t＝．　　(加3分) 　　∴当t的值为，，时，△CMQ为等腰三角形．　　(加4分)