
如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .半径为1的圆的圆心
.半径为1的圆的圆心![]() 以1个单位/
以1个单位/![]() 的速度由点
的速度由点![]() 沿
沿![]() 方向在
方向在![]() 上移动,设移动时间为
上移动,设移动时间为![]() (单位:
(单位:![]() ).
).
(1)当![]() 为何值时,⊙
为何值时,⊙![]() 与
与![]() 相切;
相切;
(2)作![]() 交
交![]() 于点
于点![]() ,如果⊙
,如果⊙![]() 和线段
和线段![]() 交于点
交于点![]() ,证明:当
,证明:当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
 |
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:阅读理解
| 4×9 |
| 4×4 |
| 2×3 |
| ab |
| 6 |
| 5 |
| 6 |
| 5 |
| 6×5 |
| 6×5 |


查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 ,
,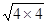 ,2+3 2
,2+3 2 。请猜想:当
。请猜想:当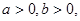 则
则
 。
。 展开
展开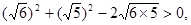 ∴6+5
∴6+5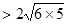 。
。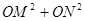 的值。
的值。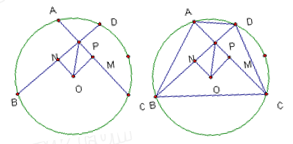
查看答案和解析>>
科目:初中数学 来源:2012届江苏省无锡市新区九年级下学期期中考试数学卷(带解析) 题型:解答题
(1)阅读理解
先观察和计算,并用“>”、“<”、“≥”、“≤”、“=”填空:4+9 2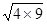 ,
,
4+4 2 ,2+3 2
,2+3 2 。请猜想:当
。请猜想:当 则
则
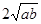 。
。
如∵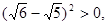 展开
展开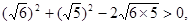 ∴6+5
∴6+5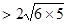 。
。
请你给出猜想的一个相仿的说明过程。
(2)知识应用
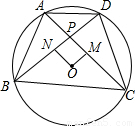
①如图⊙O中,⊙O的半径为5,点P为⊙O内一个定点,OP=2,过点P作两条互相垂直的弦,即AC⊥BD, 作ON⊥BD,OM⊥AC,垂足为M、N,求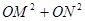 的值。
的值。
②在上述基础上,连接AB、BC、CD、DA,利用①中的结论,探求四边形ABCD面积的最大值。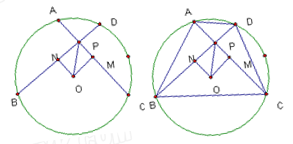
查看答案和解析>>
科目:初中数学 来源:2012年江苏省无锡市新区中考数学一模试卷(解析版) 题型:解答题
 ,
, ,2+3______2
,2+3______2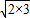 .请猜想:当a>0,b>0,则a+b______
.请猜想:当a>0,b>0,则a+b______ .
. ,展开
,展开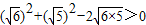 ,∴6+5
,∴6+5 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com