练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如图，一直线与两坐标轴的正半轴分别交于A、B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20，则该直线的函数表达式是（　　）
    A．y=x+10B．y=-x+10C．y=x+20D．y=-x+20

    分析 设点P的坐标为（x，y），根据矩形的性质得到|x|+|y|=10，变形得到答案．

    解答 解：设点P的坐标为（x，y），
    ∵矩形的周长为20，
    ∴|x|+|y|=10，即x+y=10，
    ∴该直线的函数表达式是y=-x+10，
    故选：B．

    点评 本题考查的是一次函数解析式的求法，掌握矩形的性质、灵活运用待定系数法求一次函数解析式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

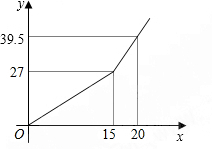    10．某市自来水公司为鼓励居民节约用水，采取月用水量分段收费方法．若某户居民应交水费y（元）与用水量x（方）的函数关系如图所示．
    （1）分别求出当0≤x≤15和x＞15时，y与x的函数关系式．
    （2）若某用户该月用水21方，则应交水费多少元？
    （3）若小明家每月水费不少于79.5元，则小明家每月用水量不少于多少方？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．在△ABC中，∠C=30°，∠A与∠B的度数比是1：2，则∠A的度数是（　　）
    A．50°B．100°C．30°D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列等式成立的是（　　）
    A．$\frac{1}{2}$=$\frac{b}{2b}$B．$\frac{b}{2b}$=$\frac{1}{2}$C．$\frac{m}{2a}$-$\frac{n}{a}$=$\frac{m-n}{a}$D．a÷b•$\frac{1}{b}$=a

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．解不等式组$\left\{\begin{array}{l}{2x+1＞-1}\\{2x+1＜3}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，直线l与x轴、y轴交于点A、B，点C为线段AB上的一动点，过点C分别作CE⊥x轴于点E，作CF⊥y轴于点F．若四边形OECF的周长为6，则直线l的表达式为（　　）
    A．y=-x+6B．y=x+6C．y=-x+3D．y=x+3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，有以下五个条件：①∠B+∠BCD=180°，②∠1=∠2，③∠3=∠4，④∠B=∠5，⑤∠B+∠BAD=180°，其中能判断AB∥CD的条件有（　　）个．
    A．4B．3C．2D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

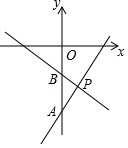    9．如图，一次函数y1=ax-9（a≠0）与y2=bx-3（b≠0）的图象交于点P，与y轴分别交于点A，B，若S△ABP=12，则关于x的不等式bx+6＞ax的解集是x＜4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．6月是某地暴雨多发季节，6月10日，某水库的水位从9：00开始持续上涨，下表记录了最近4小时内5个时间点的水位高度．
    时刻9：0010：0011：0012：0013：00
    水位高度（米）55.35.65.96.2
    设水位上长时间为x小时，水位高度为y米．
    （1）若水位按照以上上涨规律，当日14：00时，水位高度为6.5米，此时x=5小时；
    （2）试写出一个符合表中数据的y关于x的函数关系式；
    （3）该水库的最高警戒水位是7米，据统计，这祌上涨规律还会持续3个多小时，当时13：00时，驻地距离水库72千米远的武警官兵接到水库管理员的报警求救电话，防汛指挥部要求武警官兵必须在水库水位到警戒水位武警官兵接到电话后，立即从驻地出发，则他们赶往水库的速度需要什么条件？

    查看答案和解析>>

    同步练习册答案