
【题目】已知某商品的进价为每件30元,九(1)班数学兴趣小组经过市场调查,整理出该商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
第x天 | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
(1)分别求出第25天和第60天商家在销售该商品时所获得的利润;
(2)问销售该商品第几天时,当天的销售利润为6050元?
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A. 相等的角是对顶角
B. 若直线a与b互相垂直,记作a∥b
C. 内错角相等
D. 在同一平面内,过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左边到右边的变形,因式分解正确的是( )
A. 2a2﹣2=2(a+1)(a﹣1) B. (a+3)(a﹣3)=a2﹣9
C. ﹣ab2+2ab﹣3b=﹣b(ab﹣2a﹣3) D. x2﹣2x﹣3=x(x﹣2)﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠C=∠D,OD=OC.求证:DE=CE.

【答案】证明见解析
【解析】试题分析:利用ASA证明△OBC≌△OAD,根据全等三角形的对应边相等可得OA=OB,再由OD=OC,即可得AC=BD,根据AAS证明△ACE≌△BDE,再由全等三角形的对应边相等即可得结论.
试题解析:
在△OBC和△OAD中,
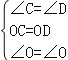 ,
,
∴△OBC≌△OAD(ASA),
∴OA=OB,
∵OD=OC,
∴OD﹣OB=OC﹣OA,即AC=BD,
在△ACE和△BDE中,
 ,
,
∴△ACE≌△BDE(AAS),
∴DE=CE.
【题型】解答题
【结束】
27
【题目】如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.
(1)求∠BCE的大小;
(2)求证:BE=AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com