
【题目】如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是______.

科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意三角形ABC,
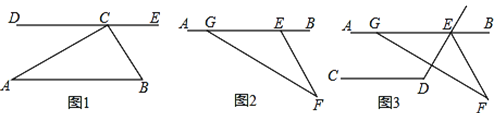
(1)如图1,过点C作DE∥AB,求证:∠DCA=∠A;
(2)如图1,求证:三角形ABC的三个内角(即∠A、∠B、∠ACB)之和等于180°;
(3)如图2,求证:∠AGF=∠AEF+∠F;
(4)如图3,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 a,b,c 分别是△ABC 的三边长.
(1)分解因式:①ac﹣bc= ,②﹣a2+2ab﹣b2= ;
(2)若 ac﹣bc=﹣a2+2ab﹣b2,试判断△ABC 的形状;并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象的顶点为A.二次函数
的图象的顶点为A.二次函数![]() 的图象与x轴交于原点O及另一点C,它的顶点B在函数
的图象与x轴交于原点O及另一点C,它的顶点B在函数![]() 的图象的对称轴上.
的图象的对称轴上.
(1)求点A与点C的坐标;
(2)当四边形AOBC为菱形时,求函数![]() 的关系式.
的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,O 是等边三角形 ABC 内一点,连接 OA,OB,OC,且 OA=3,OB=4,OC=5,将△BAO 绕点 B 顺时针旋转后得到△BCD,连接 OD.
填空:①旋转角为 °;②线段 OD 的长是 ;③∠BDC= °;
(2)如图 2,O 是△ABC 内一点,且∠ABC=90°,BA=BC. 连接 OA,OB,OC,将△BAO 绕点 B 顺时针旋转后得到△BCD,连接 OD.当 OA,OB,OC 满足什么条件时,∠BDC=135°?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).

(1)请在网格平面内作出平面直角坐标系;
(2)将△ABC平移至△DEF,使得A、B、C的对应点依次是D、E、F,已知D(2,3),请在网格中作出△DEF;
(3)若Q(a,b)是△DEF内一点,则△ABC内点Q的对应点点P的坐标是 (用a、b表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场的打折活动规定:凡在本商场购物,可转动转盘一次,如图,并根据所转结果付账.

(1)分别求出打九折,打八折的概率;
(2)求不打折的概率;
(3)小红和小明分别购买了价值200元的商品,活动后一共付钱360元,求他俩获得优惠的情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com