
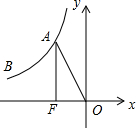
 如图,已知反比例函数的图象经过点A(-2,4)、B(m,2),过点A作AF⊥x轴于点F,连接OA.
如图,已知反比例函数的图象经过点A(-2,4)、B(m,2),过点A作AF⊥x轴于点F,连接OA.分析 (1)直接把点A(-2,4)代入y=$\frac{k}{x}$求出k的值即可得出其函数解析式,再把点B(m,2)代入即可得出m的值;
(2)先求出F点的坐标,再根据直线l过点O且分△AFO的面积1:2可知直线l过点(-2,$\frac{4}{3}$)或点(-2,$\frac{8}{3}$),再利用待定系数法求出直线l的解析式即可.
解答 解析:(1)∵把A(-2,4)代入y=$\frac{k}{x}$,得k=-2×4=-8,
∴反比例函数的解析式为y=-$\frac{8}{x}$.
∵把B(m,2)代入y=-$\frac{8}{x}$得,2m=-8,
∴m=-4;
(2)∵A点坐标为(-2,4)、B点坐标为(-4,2),而AF⊥x轴,
∴F点坐标为(-2,0).
∵直线l过点O且分△AFO的面积1:2,
∴直线l过点(-2,$\frac{4}{3}$)或点(-2,$\frac{8}{3}$).
设直线l的解析式为y=kx(k≠0),
①把点(-2,$\frac{4}{3}$)代入y=kx得,$\frac{4}{3}$=-2k,解得k=-$\frac{2}{3}$,
∴直线l的解析式为y=-$\frac{2}{3}$x.
②把点(-2,$\frac{8}{3}$)代入y=kx得,$\frac{8}{3}$=-2k,解得k=-$\frac{4}{3}$,
∴直线l的解析式为y=-$\frac{4}{3}$x.
综上所述,直线l的解析式为y=-$\frac{2}{3}$x或y=-$\frac{4}{3}$x.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 周末,小军(用A表示),小明(用B表示),小华(用C表示)和小张(用D表示)一起到图书馆看书,圆桌旁边有四个座位,A先坐在如图所示的位置上,B,C,D三人随机坐到其他三个座位上,则A与B对面而坐的概率为$\frac{1}{3}$.
周末,小军(用A表示),小明(用B表示),小华(用C表示)和小张(用D表示)一起到图书馆看书,圆桌旁边有四个座位,A先坐在如图所示的位置上,B,C,D三人随机坐到其他三个座位上,则A与B对面而坐的概率为$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a2b-a2b=2 | |
| B. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| C. | 单项式-x2的系数是-1 | |
| D. | 若分式$\frac{{{a^2}-1}}{a+1}$的值等于0,则a=±1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,C为⊙O上一点,AD垂直于过C点的直线,垂足为D,AC平分于∠DAB.
如图,AB为⊙O的直径,C为⊙O上一点,AD垂直于过C点的直线,垂足为D,AC平分于∠DAB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com