
【题目】△ABC的一边长为5,另两边长分别是二次函数y=x2﹣6x+m与x轴的交点坐标的横坐标的值,则m的取值范围为
【答案】2.75<m≤9
【解析】解:由根与系数的关系可得:x1+x2=6,x1x2=m,由三角形的三边关系可得:|x1﹣x2|<5,
∴(x1﹣x2)2<25.
∴(x1+x2)2﹣4x1x2<25,即:36﹣4m<25.
解得:m> ![]() .
.
∵方程有两个实根,
∴△≥0,即(﹣6)2﹣4m≥0.
解得:m≤9.
所以答案是:2.75<m≤9.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D、E、F分别在三边上,E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△GEC=3,S△GDC=4,则△ABC的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米. 
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系. ①求抛物线的解析式; ②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分. ①求圆的半径;②要使高为3米的船通过,则其宽度须不超过多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①:在△ABC中,∠ACB=90![]() ,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
(1)求证:MN=AM+BN.
(2)如图②,若过点C在△ABC内作直线MN,AM⊥MN于点M,BN⊥MN于点N,则猜想AM、BN与MN之间有什么关系?请直接写出结论,并写出图②中的全等三角形.
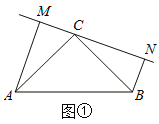
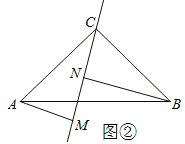
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( )

A. 67.5° B. 52.5° C. 45° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22013+22014
将下式减去上式得2S﹣S=22014﹣1
即S=22014﹣1
即1+2+22+23+24+…+22013=22014﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com